Успехи химии, т.LVII (57), №6, 1988, 944-957

УДК 539.217.5: 66.071.6

ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ ДИФФУЗИИ В ГЕТЕРОГЕННЫХ СРЕДАХ И ЕЕ ПРИМЕНЕНИЕ ДЛЯ ОПИСАНИЯ ПРОЦЕССОВ МЕМБРАННОГО РАЗДЕЛЕНИЯ

И.Н.Бекман, И.П.Романовский

В рамках единого методического подхода проведен критический анализ различных способов феноменологического описания процессов газопроницаемости гетерогенных сред: слоистых, дисперсионного типа, содержащих отдельные включения и др. Введение непрерывного геометрического фактора позволило получить обобщенные выражения для эффективных параметров переноса. Методами математического моделирования проведена проверка адекватности рассмотренного математического аппарата. Исследованы перспективы направленного подбора структуры материала для управления производительностью и селективностью газоразделительной мембраны. Библиография – 50 ссылок.

Содержание

I. ВВЕДЕНИЕ
II. ТИПЫ ГЕТЕРОГЕННЫХ СТРУКТУР И ОСНОВНЫЕ ПОДХОДЫ К ОПИСАНИЮ ДИФФУЗИИ В НЕОДНОРОДНЫХ СРЕДАХ.
III. АНАЛИТИЧЕСКОЕ РАССМОТРЕНИЕ ПРОНИЦАЕМОСТИ ДВУХКОМПОНЕНТНЫХ ГЕТЕРОГЕННЫХ МАТЕРИАЛОВ
IV. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОНИЦАЕМОСТИ ГЕТЕРОГЕННЫХ СРЕД
V. ПОДБОР СТРУКТУРЫ МАТЕРИАЛА КАК СПОСОБ УПРАВЛЕНИЯ ПРОИЗВОДИТЕЛЬНОСТЬЮ И СЕЛЕКТИВНОСТЬЮ ГАЗОРАЗДЕЛИТЕЛЬНОЙ МЕМБРАНЫ
ЛИТЕРАТУРА

I. ВВЕДЕНИЕ

В настоящее время в мембранной технологии все шире используют композитные материалы. Целенаправленный поиск таких материалов требует разработки системного подхода к конструированию мембран, обладающих заданными производительностью и селективностью, из веществ с известными диффузионными характеристиками.

Целью данного обзора является рассмотрение перспектив использования пространственной и химической организации гетерогенного материала для управления параметрами газоразделительной мембраны. Основное внимание уделено анализу существующих феноменологических теорий диффузии в неоднородных средах и проведено математического моделирования проницаемости гетерогенных сред различного типа. Даны рекомендации по выбору топологии композитного материала, обеспечивающей требуемые транспортные характеристики мембраны.

II. ТИПЫ ГЕТЕРОГЕННЫХ СТРУКТУР И ОСНОВНЫЕ ПОДХОДЫ К ОПИСАНИЮ ДИФФУЗИИ В НЕОДНОРОДНЫХ СРЕДАХ.

Способы построения математического аппарата диффузии в неоднородных средах определяются типами структур гетерогенных материалов [1-3].

В «макрогетерогенной» среде, включающей в себя неоднородности структуры, равные или превышающие длину диффузионной волны, различают механизмы последовательной диффузии (диффузия в слоистой мембране, в которой планарные неоднородности ориентированы перпендикулярно направлению потока [4], параллельная диффузия (диффузия по изолированным друг от друга канал, ориентированным вдоль направления потока [5]), диссоциативной диффузии (диффузия по взаимопроникающим сетям компонентов структуры, которую можно рассматривать как параллельную диффузию по взаимосвязанным каналам, между которыми происходит обратимый обмен атомами диффузанта [6-8] и механизм огибания диффузионным потоком отдельных крупных препятствий определенной формы и размеров [2, 8-12]. Феноменологическая теория массопереноса в средах подобного типа достаточно хорошо разработана (см. например, [1, 15]). Исключение составляет задача переноса в материалах, содержащих отдельные крупные включения произвольной формы, общее решение которой в настоящее время неизвестно. Для подобных систем отсутствуют также способы расчета эффективных коэффициентов диффузии.

Основной класс «микрогетерогенных» структур образуют дисперсионные среды, т.е. твердые тела, содержащие дисперсию включений определенной формы и размеров, которые отличаются своими термодинамическими и кинетическими характеристиками от основного материала. Под микрогетерогенной средой мы понимаем систему, негомогенности структуры которой, «дефекты», заведомо меньше длины диффузионной волны. Феноменологическая теория переноса в дисперсионных средах была предложена Максвеллом [14] для описания электропроводности дисперсий [15-18], а затем была приспособлена к задачам теплопроводности [19] и диффузии [20-21]. В данной модели сначала рассматриваются возмущения линий диффузионного потока, вызываемые отдельным препятствием заданной формы (его размеры предполагаются много меньшими по сравнению с толщиной образца), расположенным в бесконечной однородной среде, а затем – суммируются все возмущения, вызванные ансамблем включений той же формы, расположенным в образце конечных размеров. В ранних работах этот подход использовали для описания диффузии в разбавленных дисперсиях, а впоследствии его развили применительно к концентрированным дисперсиям и регулярным упаковкам включений инородных фаз [5, 22-27]. Данная теория применима для описания диффузии в средах, содержащих включения простой геометрической формы: сфера, пластина, цилиндр, эллипсоиды вращения и т.п. К сожалению, она не учитывает возможность разрыва концентрационного профиля на границе раздела включение – вмещающая среда. Модель имеет множество вариантов и в зависимости от способа суммирования возмущений приводит к различным выражениям для эффективной константы проницаемости. Эту теорию до сих пор не удалось использовать для описания нестационарного режима диффузии.

Основной класс «микрогетерогенных» структур образуют дисперсионные среды, т.е. твердые тела, содержащие дисперсию включений определенной формы и размеров, которые отличаются своими термодинамическими и кинетическими характеристиками от основного материала. Под микрогетерогенной средой мы понимаем систему, негомогенности структуры которой, «дефекты», заведомо меньше длины диффузионной волны. Феноменологическая теория переноса в дисперсионных средах была предложена Максвеллом [14] для описания электропроводности дисперсий [15-18], а затем была приспособлена к задачам теплопроводности [19] и диффузии [20-21]. В данной модели сначала рассматриваются возмущения линий диффузионного потока, вызываемые отдельным препятствием заданной формы (его размеры предполагаются много меньшими по сравнению с толщиной образца), расположенным в бесконечной однородной среде, а затем – суммируются все возмущения, вызванные ансамблем включений той же формы, расположенным в образце конечных размеров. В ранних работах этот подход использовали для описания диффузии в разбавленных дисперсиях, а впоследствии его развили применительно к концентрированным дисперсиям и регулярным упаковкам включений инородных фаз [5, 22-27]. Данная теория применима для описания диффузии в средах, содержащих включения простой геометрической формы: сфера, пластина, цилиндр, эллипсоиды вращения и т.п. К сожалению, она не учитывает возможность разрыва концентрационного профиля на границе раздела включение – вмещающая среда. Модель имеет множество вариантов и в зависимости от способа суммирования возмущений приводит к различным выражениям для эффективной константы проницаемости. Эту теорию до сих пор не удалось использовать для описания нестационарного режима диффузии.

Основной класс «микрогетерогенных» структур образуют дисперсионные среды, т.е. твердые тела, содержащие дисперсию включений определенной формы и размеров, которые отличаются своими термодинамическими и кинетическими характеристиками от основного материала. Под микрогетерогенной средой мы понимаем систему, негомогенности структуры которой, «дефекты», заведомо меньше длины диффузионной волны. Феноменологическая теория переноса в дисперсионных средах была предложена Максвеллом [14] для описания электропроводности дисперсий [15-18], а затем была приспособлена к задачам теплопроводности [19] и диффузии [20-21]. В данной модели сначала рассматриваются возмущения линий диффузионного потока, вызываемые отдельным препятствием заданной формы (его размеры предполагаются много меньшими по сравнению с толщиной образца), расположенным в бесконечной однородной среде, а затем – суммируются все возмущения, вызванные ансамблем включений той же формы, расположенным в образце конечных размеров. В ранних работах этот подход использовали для описания диффузии в разбавленных дисперсиях, а впоследствии его развили применительно к концентрированным дисперсиям и регулярным упаковкам включений инородных фаз [5, 22-27]. Данная теория применима для описания диффузии в средах, содержащих включения простой геометрической формы: сфера, пластина, цилиндр, эллипсоиды вращения и т.п. К сожалению, она не учитывает возможность разрыва концентрационного профиля на границе раздела включение – вмещающая среда. Модель имеет множество вариантов и в зависимости от способа суммирования возмущений приводит к различным выражениям для эффективной константы проницаемости. Эту теорию до сих пор не удалось использовать для описания нестационарного режима диффузии.

Казалось бы, описание диффузии в дисперсии точечных дефектов может быть получено из рассмотренных выше моделей простым уменьшением размеров включений. Однако на практике теория диффузии в дефектных средах развивалась совершенно самостоятельно путем приспособления математического аппарата, который описывает диффузию, сопровождающуюся химической реакцией диффузанта с твердым телом. Так, диффузия при наличии временного удержания диффузанта в дефектах (обратимый захват в ловушках) интерпретируется как обратимая химическая реакция 1-го порядка [32, 33], при наличии постоянного захвата – как обратимая химическая реакция 1-го порядка [34], при наличии захвата в дефектах неограниченной емкости (т.е. диффузия при наличии адсорбции в дефектах, формально подчиняющейся изотерме Ленгмюра) – как химическая реакция 2-го порядка [35-37]. В ранних работах рассматривали разбавленные дисперсии дефектов, затем перешли к существенно неоднородным средам [38, 39]. Этот подход к настоящему времени достаточно хорошо разработан: строго записаны соответствующие уравнения для 1-го и 2-го законов Фика, получены формулы для описания нестационарного массопереноса, даны выражения для описания нестационарного массопереноса, даны выражения для эффективных коэффициентов диффузии. Например, выражение для эффективного коэффициента диффузии в концентрированной дисперсии точечных дефектов учитывает коэффициенты диффузии как во вмещающей среде, так и по дефектам, а также наличие различных типов изотермы сорбции во включениях и в основном компоненте среды [39].

Особый класс образуют структуры, возникающие из разбавленных дисперсий точечных включений в ходе увеличения объемной доли последних (для краткости, в данной работе мы будем называть подобные гетерогенные тела структурами перколяционного типа) [40, 41]. Важность подобных структур обеспечивается их гибкостью, позволяющей переходить от одного из рассматриваемого типов структуры к другому.

Действительно, при малых концентрациях включений существуют дисперсии точечных дефектов. По мере роста их концентрации происходит объединение точечных включений в протяженные образования (кластеры), причем дисперсия характеризуется функциями распределения кластеров по размерам и формам. Несмотря на случайный характер кластерообразования, дисперсионная среда подобного типа подчиняется строго определенным статистическим закономерностям, и эволюция системы может быть количественно описана в рамках теории перколяции, с использованием таких понятий, как порог перколяции и критический индекс [42]. При некотором значении объемной доли возникает сквозной кластер (происходит «пробой» мембраны, сопровождающийся резкой сменой транспортных характеристик мембраны). В этом случае невозможен прямой перенос ни по одному из компонентов гетерогенной структуры (аналог слоистой среды). При дальнейшем росте объемной доли новой фазы происходит обращение фаз, т.е. уже старая фаза образует включения в новой.

Очевидно, что в зависимости от объемной доли включений диффузия в среде перколяционного типа может быть описана как «классическая» диффузия, как диффузия с обратимым захватом, как диффузия в дисперсионной среде, как диссоциативная диффузия и как диффузия в слоистой среде. Единое описание эволюции системы с диффузионной точки зрения требует объединения теории перколяции с уравнениями нестационарного переноса. Однако на этом пути встают серьезные трудности. В современном виде теория перколяции требует полного отсутствия переноса по одному из компонентов среды и применима только для описания стационарного режима проницаемости.

Подводя итоги краткого анализа известных моделей диффузии в гетерогенных средах, можно сделать следующие замечания.

1)  Существуют два основных подхода к созданию математического аппарата. Первый основан на замене гетерогенной среды на гомогенную с теми же эффективными диффузионными свойствами. Такая замена может быть проведена, если характерный размер неоднородностей структуры меньше длины диффузионной волны. Второй подход применяют для описания диффузии в средах, содержащих отдельные крупные включения, размеры которых заведомо превышают длину диффузионной волны. В данном случае учитывается пространственное расположение компонентов среды, локальные значения коэффициентов растворимости и диффузии в каждом компоненте форма и размеры включений, а также диффузионное сопротивление границы раздела фаз. К сожалению, до сих пор эти два способа описания диффузии в гетерогенных средах развивались совершенно независимо друг от друга. Более того, даже в рамах одного подхода возникли различные варианты, исходящие из фактически одинаковых физических принципов, но приводящие к различным конечным выражениям. Например, константа проницаемости Р дисперсии включений в зависимости от выбора метода усреднения концентрационного поля описывается формулами [1, 27]:

где Ф₁ и Ф2 – объемные доли компонентов 1 и 2, соответственно, Р₁ и Р₂ – константы проницаемости компонентов 1 и 2;

где ;

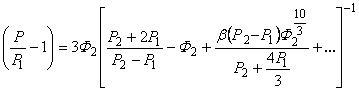
где простой кубической упаковки сфер b = 0,523 [15] (в работе [23] b  = 1,31; для объемоцентрированных кубической упаковки сфер b = 0,129 [23], а для гранецентрированной кубической упаковки b = 0,0752 [23].

Анализ этих выражений показывает, что они дают примерно одинаковые результаты при P₂ < P₁, но существенно различные при P₂ > P₁.

При таком многообразии выражений возникает естественный вопрос: какая из приведенных формул наиболее физически обоснована и универсальна. Ниже мы путем анализа известных моделей в рамках единого методологического подхода рассмотрим диффузию в различных типах гетерогенных сред: дисперсных, слоистых, содержащих отдельные включения и др. и покажем, что возникающее в результате такого анализа модифицированное уравнение Максвелла позволяет обобщить практически все известные способы описания диффузии в неоднородных средах. Адекватность подхода проверим путем сопоставления с результатами математического моделирования диффузии в гетерогенных средах [43].

2)  Практически все описанные выше типы структур представлены среди конкретных полимерных систем [44, 45]. Так, параллельная диффузия наблюдается в полимерах сферолитной структуры, когда толщина мембраны сравнима с диаметром сферолитов [46]. Последовательная диффузия имеет место в слоистых мембранах, полученных прессованием нескольких пленок с различными диффузионными характеристиками, в полимерах с химически или радиационно модифицированной поверхностью и т.п. необходимость учета искажений линий диффузионного потока возникает при исследовании композитов на основе полимеров и пористых образцов. Учет геометрической формы неоднородностей структуры необходим при работе с кристаллическими полимерами или наполненными материалами [47].

Диффузия с временным удержанием диффузанта в ловушках реализуется в стеклообразных полимерах, блоксо-полимерах и т.п. модель диссоциативной диффузии, вообще говоря, должна всегда использоваться при описании процессов массопереноса в полимерах: сам факт наличия макроцепей требует учета диффузии по двум взаимосвязанным каналам (вдоль и поперек цепей), характеризующихся различными значениями коэффициентов диффузии.

Применение теории диффузии в неоднородных средах к реальным полимерным телам часто приводит к неадекватным результатам: рассчитанные из диффузионных данных параметры формы включений не соответствуют измеренным с помощью электронного микроскопа [21]. Это связано с тем, что четкие геометрические формы дефектов структуры редко встречаются в реальных системах. Кроме того, в материалах обычно присутствует целый спектр неоднородностей структуры. В частности, подобная ситуация возникает при обращении фаз.

Указанные трудности удается преодолеть путем введения в модифицированное уравнение Максвелла непрерывного геометрического фактора, значения которого или определяются экспериментально, или рассчитываются методами математического моделирования.

3) В мембранной технологии важнейшей задачей является разработка методов направленного выбора пространственной и химической организации структуры мембраны, обеспечивающей достижение высоких значений производительности и селективности мембраны. Ниже мы распространим теорию диффузии в неоднородных средах на описание проницаемости смесей газов и продемонстрируем способ выбора пространственной структуры мембраны, оптимальной с точки зрения решения проблемы мембранного разделения газовых смесей.

III. АНАЛИТИЧЕСКОЕ РАССМОТРЕНИЕ ПРОНИЦАЕМОСТИ ДВУХКОМПОНЕНТНЫХ ГЕТЕРОГЕННЫХ МАТЕРИАЛОВ

При построении феноменологической теории массопереноса в гетерогенных средах используют следующие понятия:

• Топология среды, т.е. пространственное расположение неоднородностей (слои, включения, дисперсии включений и т.п.).
• Диффузионные свойства исходных компонентов среды (коэффициенты диффузии и растворимости в них разделяемых веществ).
• Тип изотермы сорбции диффузанта в каждом компоненте среды.
• Тип диффузионного эксперимента, т.е. некоторый набор начальных и граничных условий (в данной работе мы ограничились методом проницаемости).

  Выходными параметрами являются:

• константа проницаемости гетерогенной среды, Р, определяющая величину стационарного потока через мембрану;
• средняя концентрация диффузанта в образце;
• эффективный нестационарный коэффициент диффузии, используемый для оценки времени достижения стационарного состояния;
• вид концентрационных и кинетических и кинетических зависимостей;
•  зависимость параметра диффузии от плотности включений, их формы, от структуры гетерогенного материала (толщины и формы мембраны, размера включений и т.п.), парциального давления на входе мембраны, перепада давления на образце и др

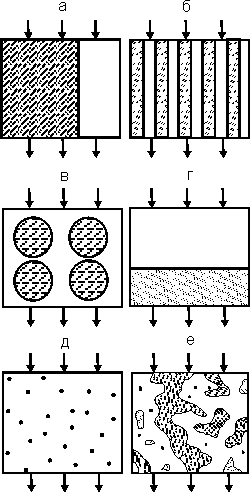Рис. 1 Основные типы гетерогенных систем [2].

Ограничимся рассмотрением пяти основных типов двухкомпонентного материала. В материале первого типа массоперенос происходит по двум изолированным друг от друга каналам, т.е. имеет место параллельная диффузия (рис.1а). В мембране второго типа возможен обратимый обмен атомами диффузанта – диссоциативная диффузия (рис.1б). Следующий тип структуры отвечает наличию в диффузионной среде включений определенной формы и размера (рис.1в, в качестве примера представлена кубическая упаковка шаров). Слоистая среда (рис.1 г) обеспечивает последовательную диффузию через слои различных компонентов. Пятым типом является структура перколяционного типа (на рис.1д представлена разбавленная дисперсия точечных дефектов, на рис.1е – дисперсия кластеров дефектов).

Процесс диффузии в однородной среде обычно рассматривают как случайное блуждание частиц диффузанта в энергетическом поле, создаваемом материалом среды (поле не изменяется при прохождении через него частицы диффузанта). Для гомогенной изотропной среды коэффициент диффузии зонда D можно представить в виде:

D = kd²

причем

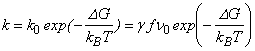
где k - константа скорости перехода атома диффузанта из одного энергетического состояния в другое; d -длина диффузионного скачка, т.е. расстояние между двумя ближайшими состояниями (потенциальными ямами, способные вместить атом зонда) в идеальной решетке; g - число путей, по которым атом зонда может покинуть потенциальную яму; f - корреляционный фактор (доля успешных скачков, вносящих вклад в хаотическую диффузию, которую будем полагать равной 1); n₀ – число скачков атомов зонда в единицу времени; DG - энергия перехода атома диффузанта из одного состояния в другое; k_B - константа Больцмана; Т – температура.

В двухкомпонентной среде имеются два типа энергетических состояний. Обозначим индексом 1 местоположение в основном материале твердого тела, а индексом 2 – местоположение в неоднородности структуры. Для описания диффузии в такой системе используем четыре константы скорости перехода k₁₁, k₁₂, k₂₁, k₂₂ и соответствующие длины диффузионного скачка d₁₁, d₁₂, d₂₁, d₂₂. Все эти параметры не зависят от концентрации диффузанта, но зависят от температуры:

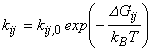
Предэкспоненциальный множитель определяется только природой диффузанта.

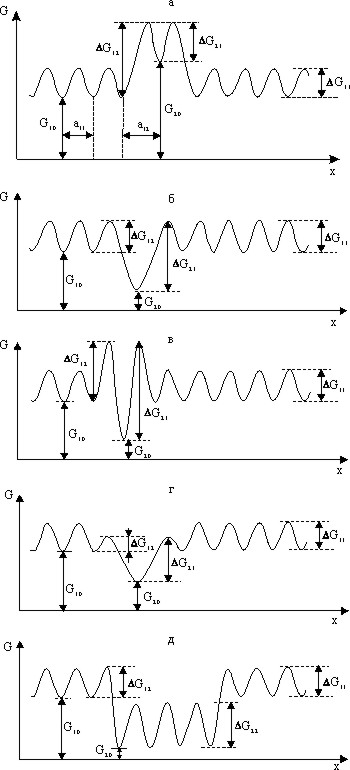Рис.2 Энергетическая диаграмма для одномерной диффузии (х – расстояние) [2].

Некоторые типы энергетических диаграмм для случая диффузии в двухкомпонентной среде приведены на рис.2. Миграция диффузанта определяется положением дна потенциальных ям типа 1 и 2 относительно нулевого уровня (т.е. энергиями G₁₀ и G₂₀), а также величиной энергетических барьеров на входе и выходе потенциальной ямы (DG₁₁  для перехода по основной матрице, DG₁₂ для перехода из основной матрицы во включение, DG₁₁ для диффузии по включению и DG₂₁ для выхода из включения в основной материал образца). Если в состоянии 2 свободная энергия выше, чем в состоянии 1 (Рис.2а), то пребывание диффузанта в состоянии 2 становится невыгодным («антиловушка») и он стремится его покинуть. Наоборот, состояние с меньшей свободной энергией (Рис.2б), самопроизвольно заполняется диффузантом («ловушка»). Переход в другую фазу может быть затруднен (DG₁₂ > DG₁₁ рис.2в), оставаться таким же, как при переходе в смежное основное состояние (рис.2б) а может быть облегчен (рис.2г) в зависимости от свойств границы раздела между состояниями 1 и 2. Если компонент 2 представляет собой протяженное включение, то на энергетической диаграмме появляются переходы типа 2 – 2 (рис.2д).

Под локальным коэффициентом диффузии понимают величину D_ij = k_ijd2ij. Отметим, что D₁₁ º D₁, D₂₂ º D₂ (где D₁ и D₂ - коэффициенты диффузии по состояниям 1 и 2), а D₁2 в общем случае не равен ни D₂₂, ни D₁₁. Таким образом, наличие дополнительных энергетических барьеров на входе в дефект приводит к трехфазной модели диффузии [48].

Величину, которая определяет отношение константы скорости перехода 1-2 к константе скорости перехода 2-1, называют по аналогии с понятиями, применяемыми при описании кинетики химической реакции константой равновесия, К.

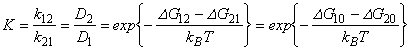
Перейдем теперь к рассмотрению заселенности энергетических состояний системы атомами диффузанта.

Введем обозначения: Ф₁ = N₁/N = V₁/V, и Ф₂ = N₂/N = V₂/V (Ф₁+Ф₂ = 1), для объемных долей компонентов 1 и 2, соответственно, где N₁ и N₂ - число состояний типа 1 и 2 (N₁+N₂ = N), V₁ и V₂ – объемы компонентов 1 и 2 (V₁+V₂ = V) композитного материала; относительные заселенности q₁ = n₁/N₁, q₂ = n₂/N₂, где n₁ и n₂ – т.е. число атомов диффузанта, находящихся в состояниях 1 и 2, соответственно); общая заселенность (растворимость) двухкомпонентной системы q = n/N=(n₁+n₂)/(N₁+N₂) и средняя заселенность зондом

Линейная изотерма сорбции описывается выражением:

q(х = 0) = К_gр₀

где К_g - константа растворимости, р₀ – парциальное давление диффузанта на входе в мембрану.

Обычно обмен атомами диффузанта между потенциальными ямами двух типов представляют в виде:

где V₁(A) и V₂(A) – атомы диффузанта в потенциальных ямах типа 1 и 2, соответственно, V₁(0) и V₂(0) - пустые состояния. Если каждый из компонентов среды характеризуется линейной изотермой сорбции, то равновесная растворимость диффузанта в первом компоненте равна q₁₀, а во втором q_20. Линейность изотермы сорбции означает, что концентрация свободных местоположений в матрице гетерогенного материала остаточно высока, т.е. относительная заселенность меньше 1. При равновесии:

n₂N₁/n₁N₂ = k₁₂/k₂₁ = K;  q₂=Kq₁

т.е. константа равновесия представляет собой отношение локальных растворимостей К=q₂/q₁. Учитывая, что относительная заселенность первого (основного) компонента не изменяется от присутствия в материале второго компонента, общая заселенность описывается выражением

Существуют различные способы экспериментального определения растворимости диффузанта в твердом теле: измерение массы образца в стационарном состоянии проницаемости, определение количества диффузанта в образце после достижения стационарного состояния, или путем деления стационарного потока диффузанта через мембрану на коэффициент диффузии, определенный по времени запаздывания. В гомогенном материале все эти методы дают одинаковые результаты, причем растворимость, измеренная методом проницаемости, равна половине величины, определенной по равновесной сорбции. В отличие от этого, для гетерогенной среды подобной закономерности не наблюдается, хотя соотношение q₂=Кq₁ всегда справедливо.

Перейдем к рассмотрению величины проницаемости, т.е. константы пропорциональности между стационарным потоков диффузанта через мембрану и разностью парциальных давлений на входе и выходе мембраны. введем обозначения: c₂ = Р₂/Р1 и c = Р/Р₁. теперь можно привести к единой форме записи известные выражения для диффузии в гетерогенных средах.

Для диссоциативной диффузии и ее частного случая – параллельной диффузии:

Для дисперсии включений одинаковой формы и размера (модифицированная формула Максвелла):

где a = a₀/(a₀-1+c₂), a₀ – геометрический фактор, зависящий только от формы включения. Для некоторых простых форм включений его можно рассчитать аналитически: например, а₀=3 для включений сферической формы, а₀= 2 для включений в форме цилиндра, расположенного перпендикулярно диффузионному потоку и т.д. Уравнение (2) справедливо для разбавленных суспензий (Ф₂ < 0,3); при переходе к плотнейшей упаковке включений в формулу (2) необходимо ввести дополнительные члены [1]. в целом уравнение (2) выполняется до тех пор, пока еще сохраняется определенность формы включения и возможны сквозные диффузионные потоки по одному из компонентов гетерогенной среды. Важно подчеркнуть, что при обращении фаз (т.е. когда матрица и включение меняются ролями) возможно появление «гистерезиса» проницаемости.

Для слоистого материала средняя концентрация диффузанта (растворимость) в мембране при стационарном состоянии проницаемости описывается выражением [4]:

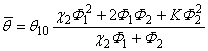
а проницаемость равна:

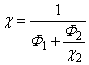(3)

Использованная в данной работе единая форма записи проницаемости основных типов структур наглядно показывает общий характер модифицированной формулы Максвелла (2), из которой остальные модели диффузии возникают как частные случаи при соответствующем выборе параметра геометрической формы а₀ (а₀ ³ 1). Крайними случаями являются параллельная диффузия (а₀ = ∞) и последовательная диффузия (а₀=1). Такой подход позволяет распространить применение формулы Максвелла, выведенной для случая включений простой формы (дискретные целочисленные значения а₀), на случай включений произвольной структуры (непрерывные дробные значения а₀). Методами численного моделирования можно найти величины а₀ для включений, имеющих «экзотическую» форму брусков в виде прямоугольника, креста и т.п., для слоистой среды с переменной границей раздела, а также изучить эволюцию а₀ в ходе обращения фаз, осуществляемую в результате зарождения зародышей, роста зародышей новой фазы, зарождения и роста зародышей и т.д. Величина а₀ является мерой искажений линий тока, т.е. линий, вдоль которых произведение коэффициента диффузии на градиент концентрации диффузанта остается постоянным: при заданном c₂ искажение тем больше, чем меньше а₀.

При анализе проницаемости разбавленной дисперсии точечных включений возникают существенные трудности, связанные с исчезновением при малых Ф₂ диффузии по второму компоненту среды. В таких структурах транспортные свойства материала определяются в основном характеристиками межкомпонентных границ. Согласно статистическому подходу [38], можно записать в принятых нами обозначениях;

С учетом равенства D12=KD21 имеем;

(4)

полученные выражения справедливы для любых значений Ф₂, т.е. подходят для описания проницаемости точечных включений в ходе полной инверсии фаз, осуществляемой «перколяционным» способом.

IV. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОНИЦАЕМОСТИ ГЕТЕРОГЕННЫХ СРЕД

Рассмотренные ранее аналитические подходы к описанию диффузии в гетерогенных средах справедливы только при различного рода допущениях и имеют ограниченное применение. Поэтому для решения таких задач проницаемости гетерогенных сред как перенос в композите, содержащем концентрированную дисперсию включений, или в среде, содержащей включения неправильной формы; при сложном характере распределения неоднородностей по толщине образца; при наличии специфических энергетических барьеров на входе во включение и т.п. следует использовать численные методы математического моделирования [43].

В работе [43] проведено моделирование диффузии в системах с линейными изотермами сорбции на основе статистического подхода, описанного выше. Весь гетерогенный материал разделяли прямоугольной сеткой на отдельные ячейки, соответствующие различным диффузионным состояниям; затем задавали матрицу энергетических переходов DG_ij и исходя из нее рассчитывали константы скорости обмена между диффузионными состояниями различного типа k_ij. После задания начальных и граничных условий полученную систему линейных дифференциальных уравнений решали методом Монте-Карло с постоянным шагом во времени.

Программа [43] предназначена для моделирования массопереноса в двумерной гетерогенной среде с произвольной топологией включений в различных диффузионных экспериментах с использованием методов проницаемости, сорбции, десорбции, метода концентрационных волн, локального диффузионного зондирования и др. В ходе расчета индицируют распределение концентрации диффузанта по гетерогенной среде, суммарные и локальные потоки по внешним границам образца, находят общую заселенность образца диффузантом (растворимость). Программа также позволяет проводить обработку кинетических зависимостей с целью определения нестационарного эффективного коэффициента. В случае среды «перколяционного» типа программа обеспечивает проведение кластерного анализа включений, определение открытой, сквозной, замкнутой пористости, нахождение среднего размера включений [43]. Проверка программы, проведенная для гомогенной среды, показала высокую точность расчета всех выходных параметров (~0,1%), а также выполнение постулированных зависимостей k_ij = f(DG_ij).

Моделирование диффузии в гетерогенных средах проводили для широкого набора параметров К, c₂ и F₂ для всех рассмотренных выше структур. На первом этапе исследовали ситуации, для которых известны аналитические выражения, на втором – ситуации, для которых отсутствует феноменологическая теория диффузии.

Проверка известных в литературе моделей показала, что только для случаев параллельной и диссоциативной диффузии, а также для диффузии в слоистой среде, имеется строгое математическое описание. При наличии протяженных включений определенной формы и размера аналитическое описание возможно для некоторых простых форм (сфера, цилиндр, сфероид), для которых «экспериментальные» значения а0 совпадают с теоретическими и при Ф₂ £ 0,3. Обнаружено, что с ростом Ф₂ аналитическая формула все хуже описывает процесс, причем c стремится к c₂ быстрее, чем предсказывает теория. Нами получено подтверждение [34] существования диффузионного гистерезиса, заключающегося в том, что проницаемость гетерогенного материала при одинаковом составе зависит от способа его получения, а именно от того, готовили дисперсию компонента 2 в компоненте 1 или наоборот. Подтвердилось также предположение о том, что геометрический параметр а₀ зависит не только от отношения ширины включения к его длине, но и от «искажающей способности» данной формы включения относительно линий диффузионного тока. В частности, методом моделирования найдено значение а₀ = 1,55 ± 0,15 для бесконечного бруска квадратного сечения, расположенного перпендикулярно направлению потока (аналитически значение а0 для такой геометрии не может быть рассчитано). Эта величина меньше значения а₀ = 2 для цилиндра, поскольку брусок с квадратным сечением искажает линии тока диффузионного тока значительно сильнее.

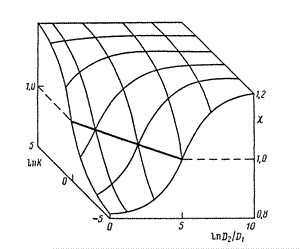Рис. 3. Зависимость проницаемости от транспортных параметров композита [2] (решетка цилиндров, а₀ = 2, Ф₂= 0,1)

Важно подчеркнуть, что влияние геометрии включений на проницаемость существенно зависит от энергетических параметров компонентов гетерогенной структуры. Типичная зависимость c от К и D₂/D₁ представлена на рис.3; в качестве примера рассмотрена проницаемость дисперсионной среды с включениями в виде цилиндра, для которого а₀ = 2, Ф₂ = 0,1. Так, при c₂ = 1 (что вовсе не означает тождества диффузионных характеристик компонентов, поскольку для линейных изотерм c₂=КD₂/D₁) проницаемость не зависит от К и D₂/D₁. При c₂=0 – случай непроницаемых препятствий – проницаемость гетерогенной среды зависит и от ее состава, и от ее геометрии:

Если же включение весьма проницаемо (пора, c®¥), то проницаемость гетерогенной среды растет в общем случае медленнее, достигая предельной величины c=1+а₀Ф₂/Ф₁.

При моделировании проницаемости дисперсии точечных включений феноменологическая модель дает только полуколичественное описание. Расхождение с теорией достигает 20-30%, однако теоретические и «экспериментальные» зависимости c(Ф₂) изменяются симбатно. Теория качественно правильно предсказывает наличие экстремумов на зависимости Р(Ф₂), а также с точностью 10% их местонахождение. Была предпринята попытка повысить точность численного расчета за счет изменения координационного числа с 4 до 8. При этом расхождение между теоретическими и «экспериментальными» результатами уменьшилась. Мы полагаем, что , хотя это и не оговорено при построении феноменологической модели [38], при статистическом суммировании потоков четырех типов неявно подразумевается координационное число, равное бесконечности. Детальный анализ этого вопроса показал, что даже при больших значениях координационного числа не удается добиться полного соответствия между теоретическими выводами и результатами математического эксперимента. Таким образом, математическое моделирование численными методами проницаемости гетерогенных сред «перколяционного» типа дает более надежные результаты, поскольку в аналитических подходах не учитывается искажение линий диффузионного потока вокруг точечных включений и их кластеров.

Зависимости проницаемости от объемной доли второго компонента для структур различных типов приведены на рис.4. Кривые c(Ф₂) практически для всех структур располагаются между двумя предельными случаями: диссоциативной или параллельной диффузии (прямая 1) и диффузии в слоистой среде (кривая 2). Исключениями являются дисперсионные структуры «перколяционного» типа (рис.1е). Как следует из (4), зависимость c от локальных транспортных параметров предусматривает влияние на перенос межкомпонентных слоев (уже упоминалось, что в данном случае возникает ситуация, требующая решение «трехфазной» диффузионной задачи для двухкомпонентной среды). В зависимости от условий на границе раздела компонентов кривая c(Ф₂) может проходить ниже прямой для предельного случая а₀ = 1, что соответствует низкой проницаемости межкомпонентного слоя (D₁₂®0, кривая 3), причем на кривой возможен минимум; может находиться целиком внутри допустимой области (проницаемость межкомпонентного слоя лежит между соответствующими значениями для компонентов среды, кривая 4) или может располагаться выше предельной прямой для а₀ = ¥. Последняя ситуация возникает при высокой проницаемости границы раздела (т.е. при D₁₂>>D₁₁, D₁₂>>D₂₂, кривая 5), причем на зависимости c(Ф₂) возможен максимум.

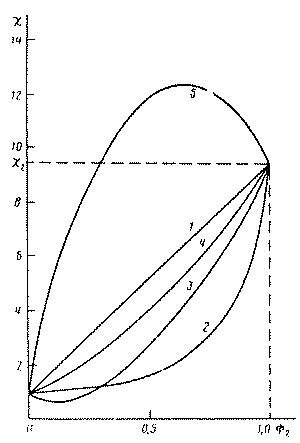Рис.4 Проницаемость структур перколяционного типа: 1 – параллельная диффузия; 2 – слоистые среды; 3-5 – перколяционые структуры с D₁₂→0 (3), D₁₁<D₁₂<D₂₂ (4) и D₁₂>>D₁₁, D₁₂>>D₂₃ (5) (по данным [43])

Помимо стационарных значений потоков численными методами [43], были получены кинетические кривые проницаемости и рассчитаны эффективные коэффициенты диффузии [49]. Не останавливаясь подробно на этих результатах, отметим, что в ряде случаев теория предсказывает возможность возникновения существенных ошибок при экспериментальном определении стационарного потока диффузанта через мембрану и, следовательно, константы проницаемости. Это связано с тем, что при определенных значениях локальных транспортных параметров может достигаться «псевдостационарное» состояние проницаемости; при временах диффузии, в 2-3 раза превышающих время запаздывания, устанавливается практически постоянный поток через мембрану (значительно ниже стационарного), что ошибочно может быть приписано достижению истинной стационарности, хотя для получения действительно стационарного потока необходимы времена в 20-30 раз более высокие.

Общая заселенность (растворимость) в структурах всех рассматриваемых типов совпадает со значениями, предсказанными теоретически.

V. ПОДБОР СТРУКТУРЫ МАТЕРИАЛА КАК СПОСОБ УПРАВЛЕНИЯ ПРОИЗВОДИТЕЛЬНОСТЬЮ И СЕЛЕКТИВНОСТЬЮ ГАЗОРАЗДЕЛИТЕЛЬНОЙ МЕМБРАНЫ

До сих пор мы рассматривали проницаемость мембран относительно какого-либо газа. Перейдем теперь к проблеме мембранного разделения смеси газов и оценим перспективы направленного подбора структуры гетерогенной среды для достижения оптимальной производительности и селективности мембраны.

Пусть на входную сторону мембраны подается смесь двух газов, процесс переноса через мембрану каждого из которых можно охарактеризовать своим набором параметров D, K, c и q. Эти параметры зависят от состава и топологии мембраны, но не зависят от состава газовой смеси. Под фактором селективности будем понимать отношение:

где c' и c'' - проницаемости для 1-го (целевого) и 2-го газов соответственно, a_i – факторы селективности исходных компонентов, a_i = Р_i'/P_i''.

Эффективность действия системы газоразделения характеризуется двумя параметрами: производительностью (т.е. проницаемостью для целевого компонента c'), определяющей его чистоту. Оптимизация мембранного разделения является сложной задачей, поскольку далеко не всегда можно одновременно добиться и высокой производительности, и высокой чистоты продукта. Как известно, мембранное разделение можно использовать либо для очистки прошедшего через мембрану потока, либо для концентрирования целевого продукта над мембраной. Естественно, что в этих случаях требования к выбору c'' и a различны. Если целевой продукт – прошедший через мембрану газ, то следует стремиться к большим значениям c' и a. В противном случае, наоборот, требуются низкие c' и a.

Влияние локальных параметров переноса гетерогенной среды на поток целевого компонента c' и на фактор селективности a различно: уменьшение D₂'/D₁' и K' приводит к уменьшению c' и a, а уменьшение D₂''/D₁'' и К'', не изменяя c' увеличивает a. Поскольку изменение c' и a в гетерогенных структурах разного типа происходит неодинаково, то в зависимости от того, работает ли мембрана на очистку или на концентрирование, эти параметры имеют оптимальные значения при совершенно различных пространственных организациях материала. Как следует из уравнения (6), a является функцией шести параметров (если считать одним из них топологический фактор а₀). Поэтому мы ограничимся лишь несколькими примерами.

Влияние топологии и локальных транспортных параметров на проницаемость (c') и селективность (a) гетерогенной мембраны *

* Расчет параметров c', c'', и a для газовых смесей № 1 и № 2 выполнен нами на основании экспериментальных данных работы [50]: смесь газов № 3 — модельная.
**Ф2 = 0,3; обозначения: 1 —параллельная диффузия, II —дисперсия цилиндров, III —слоистая среда, IV—дисперсия точечных включений.

Первые два примера заимствованы из работы [50], в которой измерялась газопроницаемость блоксополимеров ПВТМС (компонент 1) — ПДМС (компонент 2) различного состава (здесь ПВТМС—поливинил-триметилсилан, ПДМС—полидиметилсилан). Рассмотрим газовые смеси Kr—Хе и Н₂—Хе, транспортные параметры которых приведены в таблице (задача разделения подобных газовых смесей возникает в системе газоочистки АЭС). Там же представлены экспериментальные [50] и рассчитанные нами для различных структур значения стационарных потоков и факторов селективности. В случае смеси Кr—Хe экспериментально найденная селективность (a=0,56) близка к рассчитанной теоретически (0,61) для механизма параллельной (диссоциативной) диффузии (таблица, смесь газов № 1). Однако наблюдается существенное расхождение между экспериментально измеренными (2,04) и теоретически рассчитанными (10,4) значениями c'. Возможно, это объясняется возникновением дополнительных транспортных сопротивлений на границах раздела между компонентами блок-сополимсра. В данном случае использованная в эксперименте мембрана близка к оптимальной с точки зрения концентрирования Кr. При использовании мембраны для очистки Хе можно добиться увеличения ее производительности (в 5 раз), если создать структуру, обеспечивающую диссоциативный или параллельный механизмы диффузии.

В случае смеси H₂—Хе (таблица, смесь № 2) теоретическое значение производительности по целевому веществу (Н₂) слабо зависит от структуры мембраны и близко к экспериментальной величине (диффузионное сопротивление границы раздела между компонентами для водорода, по-видимому, не играет существенной роли). Однако теоретический анализ показывает, что оптимальная с точки зрения селективности структура мембраны в эксперименте не была достигнута: в данном случае следовало использовать слоистую мембрану.

Возможность появления экстремальных зависимостей a от структуры продемонстрирована на модельном примере (таблица, смесь № 3). Здесь для получения оптимального соотношения между потоком и селективностью следует при создании структуры добиваться дисперсии цилиндров (нитей, вытянутых перпендикулярно потоку).

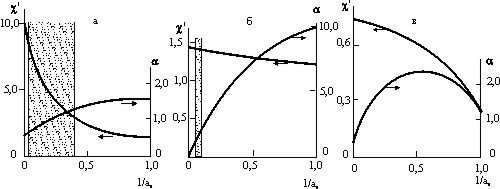Рис. 5 Диаграммы проницаемость (селективность)—топология: а —разделение смеси Кr—Хе на блок-сополимере ПВТМС—ПДМС [50] б — разделение смеси H2—Xe на блок-сополимере ПВТМС—ПДМС [50); а — модельный пример (смесь газов № 3 из таблицы) [43]

Если же необходимо сконцентрировать над мембраной газ 1, а газ 2 пропустить через нее, то лучше организовать последовательную диффузию (т. е. изготовить мембрану в виде слоев, ориентированных перпендикулярно потоку).

Влияние структуры на параметры газоразделения c' и a. удобно изучать с помощью предложенных нами диаграмм топология — свойства. При построении таких диаграмм (рис. 5) по оси абсцисс откладывают величину, обратную геометрическому фактору а₀ (значение l/а₀ изменяется от 0, что соответствует отсутствию возмущении линии тока, до 1, т. е. до величины, отвечающей сильному возмущению), по осям ординат откладывают c' и a.

Прежде всего эти диаграммы позволяют оценить на основе данных по газопроницаемости геометрический фактор а₀. Экспериментально а, можно определить, измеряя либо производительность мембраны, либо фактор селективности. Совпадение значений а₀, найденных разными способами, свидетельствует об отсутствии сопротивлений на границе раздела компонентов. Расхождение значений а₀, полученных по c' и a (область неопределенности а₀ на рис. 5 заштрихована), и случае смеси Кr—Хе (рис. 5, a) велико и намного больше соответствующей области для смеси Н₂—Хе (рис. 5, б).

Таким образом, подобные диаграммы могут быть использованы для целей диффузионно-структурного анализа, т. е. для определения топологических особенностей мембраны, используемой в процессе разделения. С другой стороны, их можно применить для выбора оптимальной структуры газоразделительных мембран, поскольку при известных транспортных характеристиках исходных компонентов они наглядно отражают свойства любых гетерогенных структур. В представленном на рис. 5, а случае, выбор структуры позволяет управлять в основном производительностью мембраны, изменяя ее на порядок; в то же время селективность изменяется при этом всего в 1,5 раза. Рис. 5, б иллюстрирует обратный пример: структура мембраны управляет в основном селективностью, оставляя производительность почти постоянной. Более сложный вариант показан на рис. 5, в. В этом случае изменение топологии приводит, как уже указывалось выше, к экстремальным значениям a. Область достижения экстремума наглядно видна на диаграмме. Анализ целевых функций c' и a позволяет быстро оценить, например, потерю производительности мембраны при увеличении селективности; имеется также возможность введения единой целевой функции, для построения которой требуется дополнительная информация о конкретном химико-технологическом процессе.

ЛИТЕРАТУРА

1. Barrer R. М.//Diffusion in Polymers/Eds Crank J., Park G. S. N. Y.: Acad. Press. 1968. P. 165.
2. Бекман И. //.//Взаимодействие водорода с металлами/Под ред. Захарова А П. М.: Наука, 1987, С. 143.
3. Бекман И. И. Диффузия в дефектных средах//Балек В., Тельдеши Ю. Эманационно-термический анализ. М.: Мир, 1986. С, 315.
4. Ваrrie J. A., Levine J. D; Michaels A. S„ Wong P.//Trans. Faraday. Soc. 1963. V. 59. P. 869.
5. Сидоренко В. М., Сидорак И. И.//Физико-химич. механика материалов. 1973. Т 9. С. 52.
6. Кучер Т. И./ /Физика твердого тела. 1964. Т. 6. С. 623.
7. Купряжкин А. Я; Губанов В. ., Плетнев Р. /Н/., Швейкин Т. //.//Дефекты и диффузия газов в кристаллах. Свердловск. Изд. УНЦ АН СССР, 1985. С. 220.
8. Бекман И. Н., Габис И. Е., Компаниец, Т. Н. и др.//0бзоры по электронной технике. 1985. Сер. 7. Вып. 1. С. 37.
9. Криштал М. А.//Механизм диффузии в железных сплавах. М.: Металлургия. 1972. 400 с.
10. Тихонов А. Н., Самарский А. А. //Уравнения математической физики. М., 1966. С, 686.
11. Райченко А. //Математическая теория диффузии в приложениях. Киев: Наук. думка, 1981. С. 355.
12. Kapcлоу Г.. Егер Д.//Теплопроводность твердых тел. М.: Наука, 1962. 487 с.
13. Николаев Н. И.//Диффузия в мембранах. М.: Химия, 1980. С. 76.
14. Maxwell J. C.//Treatise on Electricity and Magnetism. Oxford: University Press, 1904. V. 1. P. 44.
15. Runge J.//Z. Techn. Phvs. 1925. V. 6. P. 21.
16. Fricke H.//Physics. 1931. V. 1. P. 106.
17. Bruggeman D. H. G.//Annal. Phys. 1935. В. 5. S. 24.
18. Bruggeman D. H. G.//Ibid. 1935. P. 5. S. 636.
19. Mitoff S. P.//Adv. Mater. Res. 1969. V. 3. P. 305.
20. Klute С. H.//J. Appl. Polym. Sci. 1959. V. la. P. 340.
21. Michaels A. S.. Bixler H. J., Fein H. L.//J. Appl. Phys. 1964. V. 35. P. 3165.
22. Rayleigh J. W.//Phil. Wag. 1892. V. 34. P. 481.
23. De Vries D. A. //Thermal Conductivity of Gramеlar Materials Bull. Inst. Intern, du Froid, Paris. 1952. P. 3.
24. Bottcher С.J.//Rec. Trav. Chim. Pays-Bas. Belg. 1945. V. 64. P. 47.
25. Polder D., Van Santcn J. H.//Physica s Grav. 1946. V. 12. P. 247.
26. Barrie J. А., Мunday K.//Membran. Sci. 1983. V. 13. P. 175.
27. Barrie J. A., Ismail J. B.//Ibid., 1983. V. 13. P. 197.
28. Золотарев П. П., Дубинин. И. М.//Докл. АН СССР. 1973. Т. 220. С. 136.
29. Ruckenstein E., Vaidynaychan A. S., Younggust G, R.//Chem. Eng. Sci. 1971. V. 26. P. 1305.
30. Чалых А. Е., Улин В. И., Золотарев П. П. и др.//Изв. АН СССР. Сер. хим. 1976. С. 735.
31. Волощук A. М„ Золотарев П. П.. Улин В. И. //Изв. АН СССР. Сер. хим. 1974. С. 1250.
32. Hurst D. G. GRRP-1124. Atomic Energy of Canada. Chalk River (Ontario). 1962.
33. Gaus H.//Z. Naturforsh. 1905. В. 20а. S. 1298.
34. Danckwerts P.V.//Trans. Faraday Soc. 1951. V. 47. P. 1014.
35. McNabb A., Foster P.R.//TMS AIME. 1963. V. 227. P. 618.
36. Oriani R. A. //Acta Metall. 1970. V. 15. P. 137.
37. McLellan R. B.//lbid. 1979. V. 27. P. 1655.
38. Barrer R. M.//J. Membrane Sci. 1984. V. 18. P. 25.
39. Bhatia D.. Vieth М. R.//lbid. 1980. V. 6. P. 351.
40. Rroudbent S. R., Hammersley J. M.//Proc. Camb. Phil. Soc. 1957. V. 53. P. 629.
41. Kirkipatrik S.//Rev. Mod. Phys. 1973. V. 45. P. 574.
42. Mohanty К. К; Otiino J. M„ Davis H. T.//Chem. Eng, Sci. 1982. V. 37. P. 905.
43. Романовский И. П., Бекман И. Н. //Вестник МГУ. Сер. химия. 1981. Т. 22. С. 517.
44. Рейтлингер С. А. //Проницаемость полимерных материалов. М.: Химия, 1987. С. 161.
45. Чалых А. Е.//Диффузия в полимерных системах. М.: Химия, 1987. С. 161.
46. Косова 3. П., Рейтлингер С. /Высокомолекуляр. соединения. 1967. Т. 9. А. С. 415.
47. Kpейтус А. Э; Чалых А. Е., Вятере Э. Ф., Вархалис А. Ю.//Модификация полимерных материалов. Рига: Изд-во РПИ, 1978. С. 35.
48. Овчинников Л. А., Тимашев С. Ф., Белый А. А. //Кинетика диффузионно-контролируемых процессов. М.: Химия, 1986. С. 203.
49. Швыряев А. А., Бекман И. Н.//Вестник МГУ. Сер. химия. 1981. Т. 22. С. 517.
50. Иевлев А. Л. Тепляков В. В., Дургарьян С. Г., Наметкин Н. С.//Докл. АН СССР. 1982. Т. 264. С. 1421.