М(Н) + Д(0)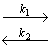 Д(Н)
+ М(0),
Д(Н)
+ М(0),
(5.1)
АКАДЕМИЯ НАУК СССР
Программный комитет «Физика, химия и механика поверхности»
Институт физической химии АН СССР
Ответственный редактор
доктор физико-математических наук А. П. ЗАХАРОВ
МОСКВА «НАУКА»
1987
И. Н. БЕКМАН
Диффузия в микрогетерогенных средах
1.1. Константа равновесия
1.2. Эффективный коэффициент диффузии
1.3. Миграция по нескольким взаимосвязанным каналам при ограниченной емкости всех каналов
1.4. Многоканальная диффузия с обратимым обменом
1.5. Диффузия с временным удержанием при ограниченной емкости как диффузионных путей, так и ловушек
1.6. Диффузия с обратимым захватом
1.7. Диффузия при наличии постоянного захвата
Диффузия в диперсионных средах
2.1. Кинетика диффузии
2.2. Обтекание диффузионным потоком отдельных препятствий
2.3. Эффективный коэффициент диффузии в среде дисперсионного типа
Следствия теории диффузии в дефектных средах и их экспериментальная проверка
Хорошо известно, что водород, диффундирующий в кристаллической решетке металла, способен взаимодействовать с различного рода дефектами, содержащимися в реальных твердых телах [1]. Наличие подобных взаимодействий приводит к изменению значений определяемых экспериментально параметров растворения и диффузии, а также к появлению таких аномалий, как изменение формы кинетической кривой, зависимость эффективных коэффициентов диффузии от давления водорода, толщины образца, времени диффузионного эксперимента, изломы на аррениусовских зависимостях и т. п. Такие эффекты проявляются уже на чистых металлах, но особенно они заметны при введении примесей. Накопление водорода в дефектах металла вызывает значительное ухудшение эксплуатационных характеристик материала. В то же время, направленное введение ловушек является эффективным способом борьбы с водородной хрупкостью [2]. Поэтому изучение процессов взаимодействия водорода с несовершенствами структуры металла представляет большой практический интерес.
Реальные твердые тела никогда не обладают однородной структурой; обычно они содержат широкий набор дефектов как равновесных (вакансии, междоузлия), так и неравновесных (границы зерен, дислокации, включения инородных фаз и т. п.). Поэтому при создании даже простейшей теории диффузии в двухкомпонентной системе, содержащей лишь диффузионные пути и один тип дефектов, приходится учитывать плотность дефектов (точнее, распределение дефектов по толщине образца), энергетические характеристики (глубины потенциальных ям и высоты разделяющих их энергетических барьеров), геометрию и размеры дефектов, их пространственную ориентацию и т. п. В общем случае для описания гетерогенной структуры необходимо ввести функции распределения (по размерам кластеров дефектов, энергиям активации и т. п.). Кроме того, микроструктура существенным образом зависит от температуры эксперимента и может изменяться при внешних воздействиях (например, механической деформации) или в ходе твердофазных процессов (например, фазовых переходах). Очевидно, что диффузия в реальных материалах должна характеризоваться спектрами значений локальных коэффициентов диффузии и констант растворимости, зависящими от параметров взаимодействия водорода с конкретными типами неоднородности металла и от степени их доступности для диффузанта. Эти параметры, в свою "очередь, определяются размером и эффективным зарядом атома диффузанта. Важным обстоятельством является тот факт, что водород, растворяющийся в металле, существенным образом изменяет его микроструктуру.
Полное описание диффузии водорода в дефектных средах сводится к решению систем нелинейных дифференциальных уравнений с координатной, временной и концентрационной зависимостями параметров диффузии. Решение подобных задач представляет собой сложную проблему, и на практике ограничиваются построением простых математических моделей, учитывающих какие-либо характерные особенности структуры образца. Известны подходы, рассматривающие огибание диффузионным потоком отдельных препятствий; диффузию в микрогетерогенной среде, содержащей точечные дефекты; диффузию в дисперсных средах, составленных из включений определенных размеров и формы; диффузию по сети дефектов и др. В данной главе мы коротко рассмотрим некоторые из них.
Рассмотрим диффузию водорода в среде, содержащей точечные неоднородности структуры, равномерно распределенные по объему материала. Водород может быть локализован в двух энергетических состояниях: в ненарушенной матрице металла (например, в междоузлиях) — состояние 1 или в дефектах (например, вакансиях) — состояние 2. Реакцию обмена атомами диффузанта между двумя типами потенциальных ям представим в виде
|
М(Н) + Д(0) |
(5.1) |
где М(Н) — атом водорода, расположенный в междоузлии; Д(0)—пустой дефект; Д(Н) — атом водорода в дефекте; М(0) — пустое междоузлие; k1 — константа скорости реакции перехода водорода из состояния 1 в состояние 2; k2 — константа скорости обратного перехода.
Введем обозначения: С1 и С2—концентрации водорода в состояниях 1 и 2 соответственно; n1 и n2 — концентрации соответствующих типов потенциальных ям; N1 и N2 — число состояний 1и 2 (N1 + N2 = N); q1=C1/n; q2=C2/n; q= q1+ q2; Ф1=N1/N; Ф2= N2/N (Ф1 + Ф2=1); d4 и d2 — емкости потенциальных ям типа 1 и 2 соответственно (т. е. число атомов, способных разместиться в яме конкретного типа); C1m=d1n1 C2m=d2n2 — максимальные емкости потенциальных ям типа 1 и 2.
Константа равновесия реакции (1)
|
К = С2(С1m – С1)/С1 (С2m - С2) = q2 (d1Ф1- q1)/ q1 (d2Ф2 - q2) =k1/k2 |
(5.2) |
При d1=d2=1:
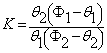
В частном случае, когда только один тип потенциальных ям (например, тип 2) обладает ограниченной емкостью (т. е. при c1<<c1m=q1n1):
|
K=C2d1/C1(C2m-C2). |
(5.2a) |
Поскольку N1@N, то за константу равновесия можно принять [3, 4]
|
KM=K/d1n1=C2/C1(C2m—C2)=k1/k2*. |
(5.26) |
Если оба типа потенциальных ям обладают неограниченной емкостью (т. е. при С1<<С1m, С2<<С2m), то
|
К=С2n1/С1n2=q2Ф1/q1Ф2=k1/k2* |
(5.2в) |
или
|
Кх = С2/С1 = k1/k2* = KФ2Ф1 |
(5.2г) |
где k1*= k1/n2; k2*= k2/n1.
Замечание. Если ввести понятие относительной заселённости дефектов атомами водорода,
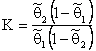 то
то
![]()
Константы, обозначенные символами К и Кx, безразмерны, КM имеет размерность, обратную концентрации.
Рассмотрим феноменологическую теорию диффузии водорода в двухкомпонентной системе, представляющей собой дисперсию точечных дефектов в «идеальной» матрице. В такой системе возможны четыре типа диффузионных скачков (табл. 5.1).
Таблица 5.1. Обозначения, используемые при анализе диффузии в микрогетерогенных средах [5]
| Диффузионный скачок | Частота скачков | Величина скачка | Коэффициент диффузии | Частота колебаний | Энергия активации диффузии |
| M→M | k11 | d11 | D11 | v11 | E11 |
| М→Д | k12 | d12 | D12 | v12 | E12 |
| Д→М | k21 | D21 | D21 | V21 | E21 |
| Д→Д | k22 | D22 | D22 | V22 | E22 |
Пусть диффузионная среда представляет собой разбавленную дисперсию точечных дефектов ограниченной емкости [5]. Тогда в стационарном состоянии диффузии поток из одного междоузлия в другое (переход типа 1→1) J11 будет пропорционален вероятности скачка в данном направлении
a11 (для изотропной среды
a=1/6), аналогично J21 пропорционален
a21. Для перехода типа 1→2 J12 определяется произведением вероятности нахождения дефекта в смежном положении с растворенным атомом водорода (комбинированная вероятность
a21Ф2) на вероятность того, что этот дефект окажется способным вместить прибывающий атом диффузанта (вероятность равна 1—![]() , где
, где
![]() =C2/C2m. Поток типа 2→2 определяется произведением вероятности нахождения двух дефектов в смежном положении (s22Ф22) на вероятность того, что смежный дефект окажется пустым (1—
=C2/C2m. Поток типа 2→2 определяется произведением вероятности нахождения двух дефектов в смежном положении (s22Ф22) на вероятность того, что смежный дефект окажется пустым (1—![]() ). Тогда частоты скачков в заданном направлении (константа скорости реакции перехода) равны:
). Тогда частоты скачков в заданном направлении (константа скорости реакции перехода) равны:
|
kll=n11a11exp(—E11/T), |
(5.3а) |
|
k2l=n21a21exp(—E21/T), |
(5.3б) |
|
kl2=n12a12Ф2exp(—E12/T), |
(5.3в) |
|
k22=n22a22Ф22exp(—E22/T), |
(5.3г) |
Коэффициенты диффузии в заданном направлении равны:
|
D11 = d112a11n11 exp (- E11/RT), |
(5.4а) |
|
D21 = d212a21n21 exp (- E21/RT), |
(5.4б) |
|
D12 = d122a12Ф2n11 exp (- E12/RT), |
(5.4в) |
|
D22 = d222a22Ф22n22 exp (- E22/RT), |
(5.4г) |
Потоки равны:
|
|
(5.5a) |
|
|
(5.5б) |
|
|
(5.5в) |
|
|
(5.5г) |
Полный поток водорода в микрогетерогенной среде
|
|
(5.6) |
Эффективный коэффициент диффузии
|
|
(5.7) |
Из уравнения (5.2б) следует, что концентрация водорода в ловушках (в местоположениях типа 2) определяется выражением
|
С2=КMС2mС1/(1 + КMС1). |
(5.8) |
Тогда
|
|
(5.9) |
При С2→С2m
![]() D→D11. Если С2<<С2m
D→D11. Если С2<<С2m
![]() , то
, то
![]() .
.
Пусть диффузионная среда представляет собой дисперсию точечных дефектов неограниченной емкости. Тогда поток в микрогетерогенной среде подобного типа
|
|
(5.10) |
Средняя концентрация (растворимость) водорода в металле
![]() , где V —объем образца
, где V —объем образца
|
|
(5.11) |
причем при наличии локального равновесия
![]() .
.
Эффективный коэффициент диффузии:
|
|
(5.12) |
где КХ=(Ф2/Ф1)К; D1= D11Ф1 + D12Ф2; D2=D21Ф1 + D22Ф2.
Из уравнения (5.9) следует, что Dэф сложным образом зависит от температуры и концентрации водорода, причем от концентрации зависит не только Dэф, но и составляющие его коэффициенты диффузии
|
D1=D11 + D12(1-С2/С2m)Ф2, |
(5.13а) |
|
D2 = D22Ф22 + D21Ф2 + D12Ф2C1/C2m |
(5-13б) |
При использовании выражения (5.9) следует учитывать, что во многих диффузионных методиках (особенно в методе проницаемости) существует значительный перепад концентраций по толщине образца. Ввиду сильной концентрационной зависимости D в подобных случаях приходится пользоваться интегральным коэффициентом диффузии:
|
|
(5.14) |
где С0 и Сl — концентрации водорода на входной и выходной сторонах мембраны соответственно.
В рассматриваемом нами случае
|
|
(5.15) |
Анализ полученного выражения показывает, что при малых концентрациях
![]() и не зависит от концентрации, но по мере роста парциального давления на входе в мембрану
и не зависит от концентрации, но по мере роста парциального давления на входе в мембрану
![]() и зависит от концентрации, а при больших парциальных давлениях водорода
и зависит от концентрации, а при больших парциальных давлениях водорода
![]() и вновь не зависит от концентрации. Отношение
и вновь не зависит от концентрации. Отношение
![]() больше или меньше единицы, если D11КMС2m меньше или больше (D21Ф2 + D22Ф22)КMС2m+ D12Ф2. Для константы проницаемости также существует два предела, причем
больше или меньше единицы, если D11КMС2m меньше или больше (D21Ф2 + D22Ф22)КMС2m+ D12Ф2. Для константы проницаемости также существует два предела, причем
|
|
(5.16) |
Выражение (5.16) на практике может быть использовано для оценки вклада D21, D22 и D12 в общий процесс переноса. Если эти вклады существенны, то константа проницаемости уменьшается по мере роста давления на входе в мембрану.
Будем рассматривать диффузию по двум каналам, между которыми происходит обмен атомами диффузанта, формально описываемый кинетикой химической реакции 2-го порядка (т. е. будем полагать, что ограниченной емкостью обладают как диффузионные пути, так и ловушки). Данный подход может быть легко обобщен на случай диффузии по n каналам [6]. Для упрощения выкладок воспользуемся выражениями (13), но пренебрежем концентрационной зависимостью D1 и D2, т. е. будем считать D1 = D11Ф1 + D12 Ф2 и D2=D21Ф1 + D22Ф2 (см. уравнение (5.12)). Система дифференциальных уравнений, описывающая диффузию в среде подобного типа, имеет вид
|
|
(5.17a) |
|
|
(5.17б) |
При наличии локального равновесия можно по уравнению (2) ввести константу равновесия и, следовательно, эффективный коэффициент диффузии
|
|
(5 18) |
Изотермы сорбции каждого вида определяются выражениями
|
|
(5.19) |
где b1 и b2 — параметры изотермы сорбции в состояниях 1 и 2 соответственно; р0 — парциальное давление водорода на входе в мембрану.
Замечание. В «классическом» случае недиссоциирующего газа изотерма Ленгмюра имеет вид:
|
|
Средняя концентрация водорода в металле
|
|
(5.20) |
или
|
|
где
![]() определяется уравнением (5.2).
определяется уравнением (5.2).
Константа проницаемости
|
|
(5 21) |
Время запаздывания в методе проницаемости (первый статистический момент от кривой «прорыва», m1=tL) при обычных граничных условиях С(0, t)=C0, С(l, t)=0, C(x, 0)=0 определяется выражением
|
|
(5.22) |
где
f0 =
(6/y3)[y2/2+y-(l+y)ln(l+y)];
f1 = (6/y3)[y/2-3y/2(l+y)+ln(l+y)/(l+y)];
f2 = (6/y3)[y/6-1/2(1+y) + 1/2(1+y)2-1/6(1+у)3];
f3 = (6/y3)[-3y/2+y/2(l+y) +(l+y)ln(l+y)];
f4 = (6/y3)[-1/2-1/2(l+y)2-ln(l+y)/y]
n = D2/D1;
a = (K-l)/C1m; y=aC10
![]() .
.
Из системы (5.17) и связанных с ней уравнений легко получить соответствующие выражения для многочисленных частных случаев.
При ограниченной емкости только одного канала (например, состояния 2) время запаздывания при проницаемости определяется уравнением (5.22), где
![]() Ф2a/Ф1 = К = b/L, y =
aCl0, L— константа растворимости водорода в «идеальном» металле (состояние 1).
Ф2a/Ф1 = К = b/L, y =
aCl0, L— константа растворимости водорода в «идеальном» металле (состояние 1).
Константа проницаемости
|
|
(5.23) |
растворимость
|
|
(5.24) |
Диффузия водорода по двум каналам, между которыми осуществляется обмен атомами диффузанта, формально описываемый кинетикой обратимой химической реакции 1-го порядка, обычно называют диссоциативной диффузией [7—9]. При условии неограниченной емкости как диффузионных путей, так и ловушек из уравнения (5.17) имеем
|
|
(5.25а) |
|
|
(5.25б) |
где D1 и D2 — коэффициенты диффузии по междоузлиям и вакансиям (или по ненарушенной решетке и сети дефектов) соответственно; k1* = k1n2 — константа скорости перехода атома водорода из канала 1 в канал 2; k2* = k2n1 — константа скорости обратного перехода.
В методе проницаемости зависимость потока водорода на выходе из мембраны от времени описывается формулой
|
J = J1 + J2, |
(5-26) |
где
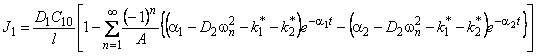 ;
;
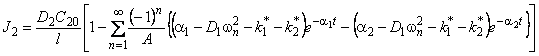 ;
;
![]() ;
;
![]() ;
a2=a1+2A;
wn=np/l
;
a2=a1+2A;
wn=np/l
Отметим, что при D2=0 выражение (5.26) описывает кинетику водородопроницаемости среды, содержащей изолированные ловушки, при k2*=0 — диффузию, сопровождающуюся необратимой химической реакцией 1-го порядка (постоянный захват). Если k1* = k2*=0, а D1¹D2, то происходит параллельная диффузия по двум независимым каналам. Время запаздывания диффузии при проницаемости
|
|
(5.27) |
При наличии локального равновесия k1*C1 = k2*C2 и
|
|
(5.27a) |
Таким образом, по мере роста константы равновесия реакции обмена время запаздывания уменьшается, переходя от значения, характерного для фазы с низким коэффициентом диффузии, к значению, характерному для фазы с высоким коэффициентом диффузии. Отметим, что при малых значениях С20 невозможно обнаружить существование высокопроводящей фазы, тогда как присутствие медленного канала обнаруживается всегда. По-видимому, именно с этим обстоятельством связан тот факт, что экспериментально не всегда удается установить присутствие макродефектов, особенно в «быстрых» мембранах. Наблюдаемый эффект тем сильнее, чем меньше значение параметра k1.
При условии локального равновесия можно ввести понятие эффективного коэффицента диффузии
|
|
(5.28) |
Очевидно, что в зависимости от отношения D1/D2 эффективный коэффициент диффузии может быть как меньше, так и больше коэффициента диффузии по идеальной решетке.
Температурная зависимость эффективного коэффициента диффузии описывается формулой
|
|
(5.29) |
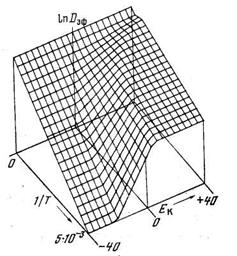 где Dэф(T) — сложная функция. Даже в простейшем случае постоянства числа диффузионных путей (т. е. Ф1 и Ф2) в зависимости от значений энергий активации диффузии EDl и ЕD2 и энтальпии реакции обмена ЕK может иметь место как уменьшение, так и увеличение эффективной энергии активации диффузии по мере роста температуры. На аррениусовской зависимости возможны изломы, причем в одних случаях тангенс угла наклона низкотемпературного участка ниже, чем тангенс угла наклона высокотемпературного участка (параллельная диффузия), а в других — тангенс угла наклона уменьшается с ростом температуры (диффузия при наличии обратимого захвата в изолированных ловушках). Более того, на аррениусовской зависимости эффективного коэффициента диффузии возможно появление максимумов и минимумов (рис. 5.1).
где Dэф(T) — сложная функция. Даже в простейшем случае постоянства числа диффузионных путей (т. е. Ф1 и Ф2) в зависимости от значений энергий активации диффузии EDl и ЕD2 и энтальпии реакции обмена ЕK может иметь место как уменьшение, так и увеличение эффективной энергии активации диффузии по мере роста температуры. На аррениусовской зависимости возможны изломы, причем в одних случаях тангенс угла наклона низкотемпературного участка ниже, чем тангенс угла наклона высокотемпературного участка (параллельная диффузия), а в других — тангенс угла наклона уменьшается с ростом температуры (диффузия при наличии обратимого захвата в изолированных ловушках). Более того, на аррениусовской зависимости эффективного коэффициента диффузии возможно появление максимумов и минимумов (рис. 5.1).
Рис. 5.1. Температурная зависимость эффективного коэффициента диффузии, рассчитанная в рамках модели диссоциативной диффузии при различных значениях энергии активации обратимого перехода из одного канала диффузии в другой
D10=10-3 см2/с; ЕD1=10
ккал/моль;D20= =0,5 см2/с, ED2=4
ккал/моль, К0=10-7
Средняя концентрация водорода в мембране
|
|
(5.30) |
Константа проницаемости
|
P=(D1+D2Kx)Ф1s1=D1s1Ф1=D2s2Ф2 |
(5.31) |
В сорбционном методе количество водорода, поглощенное пластиной ко времени t, при наличии локального равновесия на входе описывается формулой [10, 11]
|
|
(5.32) |
где
![]() ;
;
![]() ;
;
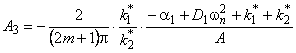
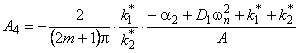
wn= (2m+1)p/l — толщина образца; S — площадь поверхности.
Поток водорода из пластины в ходе десорбции
|
|
(5.33) |
где C0 — начальная концентрация водорода в образце.
Миграция водорода в среде, содержащей дисперсию точечных изолированных друг от друга дефектов (Dl = D, D2 = 0) при ограниченной емкости как диффузионных путей, так и дефектов (кинетика такого процесса формально описывается как диффузия при наличии обратимой химической реакции 2-го порядка), определяется системой уравнений
|
|
(5.34a) |
|
|
(5.34б) |
При наличии локального равновесия
|
|
(5.35) |
где заселенность дефектов водородом найдем из уравнения (5.2), переписав его в виде
|
|
Тогда
|
|
(5.37) |
Из уравнения (5.37) следует, что в кристалле конечного размера число атомов водорода, оккупирующих один из двух типов потенциальных ям, при условии, что каждая яма способна вместить строго определенное количество атомов диффузанта, описывается распределением Ферми—Дирака. При низких температурах и низких концентрациях все атомы водорода сконденсированы на ловушках. По мере роста концентрации ловушки постепенно заполняются и после достижения условия q2 = Ф2 заполняются только диффузионные пути (рис. 5.2, а). При увеличении температуры распределение Ферми—Дирака переходит в известное распределение Больцмана [12] (рис. 5.2, б). На рис. 5.3 представлена зависимость заселенности ловушек q2 от концентрации водорода q (зависимость от Ф2 будет аналогичной) и от константы равновесия К (т. е. от температуры) при степени дефектности образца Ф2 = 0,1. Видно, что при высоких температурах (малых К) заселенность ловушек пропорциональна 0, а при низких температурах (больших К) q2 — ступенчатая функция от концентрации.
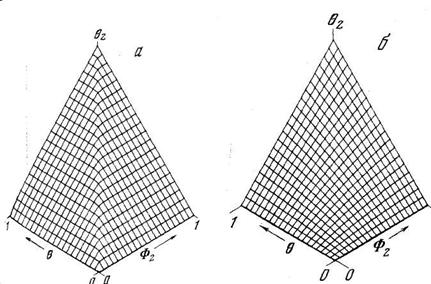 Рис. 5.2. Зависимость заселенности ловушек от общей концентрации водорода в металле и плотности дефектов
Рис. 5.2. Зависимость заселенности ловушек от общей концентрации водорода в металле и плотности дефектов
а - низкие температуры (K=1000); б — высокие температуры (K=2)
Уравнение (5.35) предсказывает концентрационную зависимость эффективного коэффициента диффузии водорода в дефектных средах, характеризующихся ограниченной емкостью ловушек и диффузионных путей. Так, при низких концентрациях (q<Ф2) основная часть атомов водорода сконденсирована на ловушках, Dэф мал и практически не зависит от концентрации; при q = Ф2 начинается перекачка атомов водорода в зону «проводимости» и Dэф возрастает по мере роста концентрации (рис. 5.4); при высоких концентрациях Dэф@D и не зависит от концентрации. Чем ниже температура эксперимента, тем сильнее проявляется концентрационная зависимость коэффициента диффузии. Формально рассчитанная энергия активации диффузии также зависит от концентрации водорода.
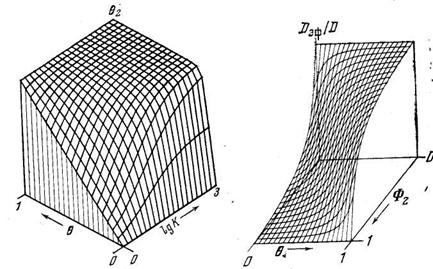 Рис. 5.3. Зависимость заселенности ловушек от концентрации водорода в металле и константы равновесия реакции захвата (температуры) при Ф2=0,1
Рис. 5.3. Зависимость заселенности ловушек от концентрации водорода в металле и константы равновесия реакции захвата (температуры) при Ф2=0,1
Рис. 5.4. Зависимость эффективного коэффициента диффузии в дефектной среде при ограниченной емкости ловушек от концентрации дефектов и общей концентрации водорода при К=10
Растворимость водорода в металле определяется уравнением (5.20). Время запаздывания при проницаемости в рамках данной модели определяется выражением [6]
|
|
(5.38) |
где
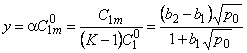 ;
;
![]()
Константа проницаемости
|
|
(5.39) |
Коротко остановимся на рассмотрении диффузии водорода в дефектной среде подобного типа при отсутствии локального равновесия. Поскольку система (5.34) является нелинейной, то ее решение возможно только численными методами. Расчеты показывают, что диффузия при наличии химической реакции 2-го порядка приводит к возникновению выпуклых концентрационных профилей (рис. 5.5), причем, чем выше концентрация диффузанта, тем сильнее искажается его форма (при больших концентрациях фронт имеет форму ступеньки).
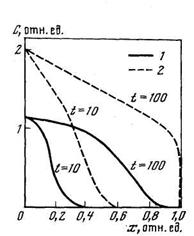 Рис. 5.5. Изменение во времени концентрации водорода по толщине мембраны при различных парциальных давлениях водорода на входе в мембрану (модель обратимого захвата при ограниченной емкости ловушек)
Рис. 5.5. Изменение во времени концентрации водорода по толщине мембраны при различных парциальных давлениях водорода на входе в мембрану (модель обратимого захвата при ограниченной емкости ловушек)
Относительная емкость ловушек s2Ф2=1; К=100; D/l2=0,01 с-1. 1 — Свх =1,2; 2 — Свх =2. Свх — концентрация диффузанта на входе в мембрану
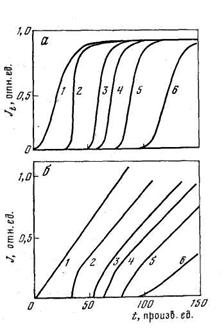 Рис. 5.6. Кинетические кривые водородопроницаемости металлов при наличии процессов обратимого захвата в ловушках ограниченной емкости
Рис. 5.6. Кинетические кривые водородопроницаемости металлов при наличии процессов обратимого захвата в ловушках ограниченной емкости
s2Ф2=1; K=100; D/l2=0,01 с-1. 1 — «классическая» диффузия без захвата; 2 — Свх=1,2; 3—1.6; 4—1,8; 5 — 2,0; 6 — Свх =3,0. а — обыкновенный масштаб; б — функциональный масштаб
Наличие захвата изменяет форму кинетических кривых диффузии. На рис. 5.6, а приведены кривые проницаемости, рассчитанные при тех же значениях параметров диффузии и захвата, что и кривые на рис. 5.5. Видно, что по сравнению с «классической» диффузией появление водорода на выходной поверхности мембраны значительно запаздывает, а затем происходит быстрое достижение стационарного состояния. Особенности кинетики диффузии в дефектных средах хорошо заметны при построении кривых проницаемости в функциональном масштабе (рис. 5.6, б), в котором классическая диффузия имеет вид прямой, выходящей из начала координат. Расчеты показывают, что в рамках данной модели кривые «прорыва» и «откачки» в методе проницаемости, кривые сорбции и десорбции не совпадают друг с другом (сорбция опережает десорбцию). На форму кинетических кривых существенное влияние оказывает функция распределения дефектов по толщине мембраны [13].
Если ограниченной емкостью обладают только дефекты, то [14—17]
|
|
(5.40a) |
|
|
(5.406) |
Тогда
|
|
(5 .41) |
где
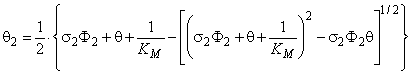 и KM определяется уравнением (5.2, б).
и KM определяется уравнением (5.2, б).
Растворимость водорода в дефектном металле описывается уравнением (5.24).
Время запаздывания при проницаемости определяется формулой (5.38) при условии, что
![]() .
.
Константа проницаемости:
![]()
Рассмотрим диффузию водорода в твердом теле, содержащем дефекты (ловушки), взаимодействующие с диффундирующим веществом. Эти ловушки улавливают диффундирующие атомы и либо некоторое время препятствуют их диффузии (временное удержание), либо вообще выводят водород из миграционного процесса (постоянное удержание). При увеличении емкости изолированных друг от друга ловушек (s2→∞) (или при увеличении концентрации ловушек (n2→∞) что, по-видимому, физически менее реалистично) система (5.40) переходит в систему уравнений диффузии при наличии взаимодействия, формально описываемого кинетикой обратимой химической реакции 1-го порядка:
|
|
(5.42a) |
|
|
(5.426) |
При наличии локального равновесия
|
Dэф = D/(l + KФ2/Ф1)= D/(l + Kx). |
(5.43) |
Эффективная растворимость определяется формулой (5.29).
Обратимый захват уменьшает величину стационарного потока водорода через мембрану в методе проницаемости (Pэф/P=Ф1), но увеличивает время запаздывания tL = l2(l + Kx/6D).
Как уже неоднократно отмечалось, наличие процессов взаимодействия водорода с дефектами приводит к сложной температурной зависимости Dэф и
![]() . Например, Dэф(Т) определяется четырьмя функциями D(Т),
s2(Т), Ф2(Т) и К(Т), связанными с соответствующими энтальпиями перехода из одного состояния в другое (рис. 5.7).
. Например, Dэф(Т) определяется четырьмя функциями D(Т),
s2(Т), Ф2(Т) и К(Т), связанными с соответствующими энтальпиями перехода из одного состояния в другое (рис. 5.7).
Коэффициент диффузии увеличивается с температурой по закону Аррениуса:
|
|
(5.44) |
где DGD
— свободная энергия миграции атома водорода по идеальной решетке металла;
DG =
DH—TSD;
DH=pV+E — энтальпия активации диффузии; р — давление; V — объем;
![]() — энтропия.
— энтропия.
Поскольку ловушка обычно глубже диффузионного пути, то константа равновесия реакции захвата убывает с ростом температуры:
|
|
(5.45) |
Поэтому даже при постоянном значении s2Ф2 на графике зависимости ln Dэф—1/T появляется излом: в низкотемпературной области энергия активации выше (Еэф=ЕD+ЕK), чем в высокотемпературной (Еэф@ ЕD) (рис. 5.8, а), т. е. аномалии, связанные с захватом, убывают по мере роста температуры. Если Ф2 — возрастающая функция (роль ловушек играют термические вакансии):
|
Ф2 = Ф20ехр(-EF/RT), |
(5.46) |
где EF — энергия активации образования вакансии, то
|
KX= (Ф2/Ф1)K=KX0 ехр(DН/RT), |
(5.47) |
где DНК=ЕК- EF
Если ЕF>ЕK, то Dэф сначала будет увеличиваться по мере роста температуры, а затем уменьшаться. В результате на зависимости Dэф—1/Т будут наблюдаться максимумы (см. рис. 5.8б).
Рассмотрим теперь кинетику нестационарной диффузии водорода в металлах при наличии временного удержания диффузанта в ловушках. В методе проницаемости зависимость потока водорода через мембрану от времени описывается выражением
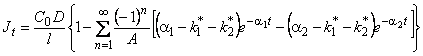 , , |
(5.48) |
где a1=1/2(k1*+k2*+Dwn2)-A; a2=1/2(k1*+k2*+Dwn2)+A; A=[k1*k2*+1/4(k1*- k2*+Dwn2)2]1/2; wn=np/l.
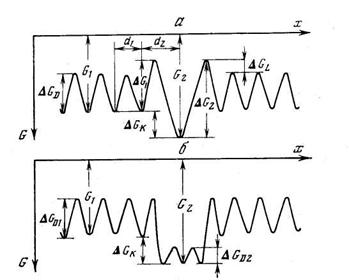 Рис. 5.7. Энергетическая диаграмма диффузионных путей и дефектов
а — точечная ловушка; б — кластер дефектов (или включение инородной фазы)
Рис. 5.7. Энергетическая диаграмма диффузионных путей и дефектов
а — точечная ловушка; б — кластер дефектов (или включение инородной фазы)
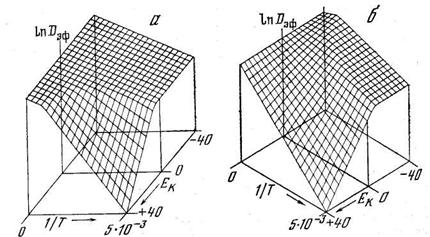 Рис. 5.8. Температурная зависимость эффективного коэффициента диффузии при различных значениях энергии активации реакции обратимого захвата (модель диффузии с временным удержанием водорода в ловушках неограниченной емкости)
Рис. 5.8. Температурная зависимость эффективного коэффициента диффузии при различных значениях энергии активации реакции обратимого захвата (модель диффузии с временным удержанием водорода в ловушках неограниченной емкости)
D0 = 10-3 см2/с; ED = 20 ккал/моль. а — К0=10-7; б — К0=107
На рис. 5.9 приведены кривые проницаемости, рассчитанные по уравнению (5.48), для различных значений параметров k1*, k2* и К. Видно, что, как и в случае ограниченной емкости ловушек, происходит запаздывание проницаемости по сравнению с диффузией в идеальной среде. Кроме того, возможно появление кривых, крайне медленно стремящихся к стационарному значению (для его достижения иногда требуются сотни времен tL, тогда как для классической диффузии достаточно 2—3tL).
Для характеристики влияния захвата на форму кинетической кривой диффузии воспользуемся методом моментов: k-й начальный момент рассчитаем по формуле
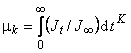 , а центральный момент Mk найдем путем переноса начала координат в точку математического ожидания. Тогда в случае проницаемости дефектной среды математическое ожидание (время запаздывания, первый начальный момент) выражается формулой
m1=tk=(l+KX)l2/6D; дисперсия кривой (второй центральный момент) —
m2=(l+KX)2l4/90D2 + KX2l2/3k2*D; асимметрия кривой (третий центральный момент) — M3 = (l+KX)3l6/420D3 + (1 + KX)2l415D2 + KXl2/ D(k2*)2.
, а центральный момент Mk найдем путем переноса начала координат в точку математического ожидания. Тогда в случае проницаемости дефектной среды математическое ожидание (время запаздывания, первый начальный момент) выражается формулой
m1=tk=(l+KX)l2/6D; дисперсия кривой (второй центральный момент) —
m2=(l+KX)2l4/90D2 + KX2l2/3k2*D; асимметрия кривой (третий центральный момент) — M3 = (l+KX)3l6/420D3 + (1 + KX)2l415D2 + KXl2/ D(k2*)2.
Из приведенных формул следует, что по мере увеличения константы захвата KX время запаздывания увеличивается, кривая уширяется и принимает более асимметричную форму (за счет появления длинного «хвоста»), tL зависит только от КX, но дисперсия и асимметрия зависят уже и от k1* и от k2*. Метод моментов дает простой способ расчета параметров D, KX, k1* и k2*; определив mk из кинетической кривой проницаемости (например, путем измерения площади, заключенной между прямой J∞ и кривой J(tk) и переходя к центральным моментам по обычным формулам математической статистики, найдем все интересующие нас величины.
В сорбционном методе количество водорода, поглощенное дефектной пластиной к моменту времени t, равно
 , , |
(5.49) |
где wm = (2m +1) p/l. В десорбционном методе зависимость потока газовыделения от времени
|
|
(5.50) |
где wm = (2m+ 1) p/l; C10, C20 — начальные концентрации водорода в подвижной и неподвижной формах соответственно.
В методе термостимулированного газовыделения изучается кинетика выделения водорода из образца в режиме программированного (как правило, линейного) нагревания. Типичные термодесорбционные спектры для образцов с различным начальным заполнением ловушек приведены на рис. 5.10. Видно, что при С10 = 1 или С20=1 кривые выделения водорода при линейном нагревании, как и в случае классической диффузии, характеризуются асимметричным пиком с крутым задним фронтом. Однако температуры максимумов, а следовательно, и рассчитанные из экспериментальных данных энергии активации диффузии существенно различны. При промежуточных значениях С10 и С20 термодесорбционные спектры имеют бимодальную структуру.
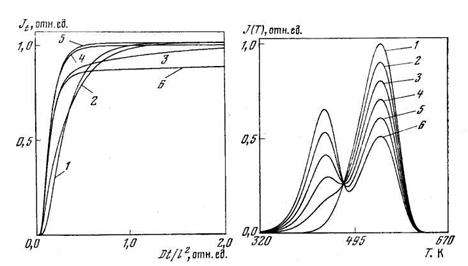 Рис. 5.9. Кинетические кривые проницаемости (кривые «прорыва») при наличии обратимого захвата водорода в ловушках неограниченной емкости
Рис. 5.9. Кинетические кривые проницаемости (кривые «прорыва») при наличии обратимого захвата водорода в ловушках неограниченной емкости
D/l2=l. K=1: J — k1 = k2= 100; 2 — 10; 3 — 1; 4 — 0,1; 5 — классическая диффузия; 6 — K=10; k1=l; k2=0,1
Рис. 5.10. Термостимулированное выделение водорода из пластины в ходе линейного нагревания в зависимости от начальной заселенности ловушек (модель временного удержания при неограниченной емкости ловушек)
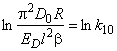 =23, Е1=Е2=ЕD=20 ккал/моль,
b=2 град/с, k2=0,1k1 К=10.
=23, Е1=Е2=ЕD=20 ккал/моль,
b=2 град/с, k2=0,1k1 К=10.
1 — С10=0, С20=1,0; 2 — 0,2, 0,8; 3 — 0,4; 0,6; 4 — 0,6, 0,4; 5 — 0,8, 0,2; 6— С10=1,0, С20=О
Пусть атом водорода, мигрирующий через вещество в ходе случайного блуждания, необратимо захватывается дефектом и тем самым выводится из диффузионного процесса. Диффузия с постоянным удержанием в ловушках описывается решением дифференциального уравнения массопереноса с учетом необратимой химической реакции 1-го порядка:
|
|
(5.51) |
где k* — константа скорости захвата водорода дефектами.
В методе проницаемости зависимость потока водорода от времени [18] определяется выражением
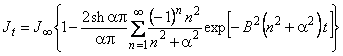 , , |
(5.52) |
где B = p2D/l;
![]() .
.
Стационарный поток водородопроницаемости равен
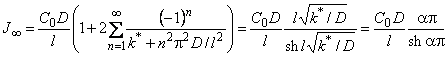 |
(5.53) |
Время запаздывания
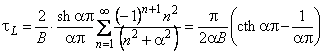 |
(5.54) |
Анализ полученных выражений показывает, что по мере увеличения интенсивности взаимодействия водорода с дефектами (т. е. при возрастании константы скорости реакции k*) значения стационарного потока и времени запаздывания уменьшаются. Химическая реакция искажает и форму кинетической кривой проницаемости: если при малых временах перенос описывается классическим законом диффузии Фика, то после точки перегиба наблюдается более крутой подъем и кривая быстрее достигает стационарного значения (которое ниже классического). По мере роста k* симметрия кривой сначала увеличивается, а затем уменьшается, но в противоположную сторону.
В сорбционном методе активные ловушки, необратимо поглощающие водород, существенно влияют на кинетику сорбции водорода металлом, причем дефектная среда поглощает большее количество диффузанта, чем «идеальная». Более того, если в случае миграции, подчиняющейся классическим законам диффузии, количество водорода в образце при больших временах стремится к постоянному пределу М∞ то при наличии ловушек постоянного удержания Mt = f(t) и при t→∞ линейно увеличивается во времени.
Кинетика сорбции описывается уравнением
 , , |
(5 55) |
где u = pD(2m+1)2/l2.
В десорбционном методе зависимость потока водорода из дефектной пластины от времени имеет вид
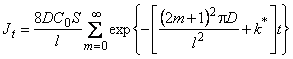 , , |
(5.56) |
т. е. газовыделение из дефектного образца заканчивается быстрее, чем из идеального. Несовпадение кинетики сорбции и десорбции является одним из основных критериальных признаков наличия в металле ловушек водорода.
Если концентрация ловушек постоянного захвата сравнима с концентрацией водорода в металле, то имеет место механизм переноса, формально описываемый как диффузия при наличии необратимой химической реакции 2-го порядка (на практике модель, учитывающая ограниченную емкость ловушек, встречается при описании некоторых процессов гидридообразования в ходе диффузии). В этом случае профиль концентрации водорода становится выпуклым, причем в стационарном состоянии проницаемости количество водорода в металле будет превышать значение 0,5 от количества водорода, поглощенного той же мембраной в сорбционном методе (классическая теория предсказывает M(∞)прон = 0,5 M(∞)сорб, стремясь к M(∞)прон = M(∞)сорб при больших значениях константы скорости взаимодействия водорода с дефектами металла). При большой интенсивности захвата в мембране образуется ступенчатый фронт концентрации, граница которого перемещается по мембране в ходе диффузионного процесса: поток на выходе длительное время отсутствует, а затем сразу достигается стационарное состояние проницаемости.
Модель диффузии в дисперсионных средах учитывает влияние геометрической формы и размеров дефектов на процессы массопереноса. Под дефектами в широком смысле понимают любые неоднородности структуры металла: газовые пузырьки, включения инородных фаз, наполнители и т. п.
Пусть включения инородных фаз имеют размеры значительно меньшие, чем толщина образца, и диффузия в дефекты сферически симметрична. На границе дефекта существует локальное равновесие. Включение действует как сток, причем по мере заполнения ловушки ее эффективность падает. Система уравнений для диффузии в пластине толщиной l=2h, содержащей включения сферической формы радиуса r0, имеет вид [19]
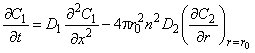 , , |
(5.57) |
|
|
(5.57б) |
| С2 = КС1, | (5.57в) |
где С1, С2 — концентрации водорода в матрице и во включении; D1, D2 — коэффициенты диффузии в дисперсионной среде и дисперсной фазе соответственно; К— локальная растворимость во включении (отношение константы растворимости водорода в «дефектной» области к константе растворимости в матрице); n2 — плотность включений.
Кинетика водородопроницаемости описывается формулой
 , , |
(5.58) |
гдеxmn определяется решением уравнения
|
|
(5.59) |
Здесь W= D2l2/D1r02; b = dD2l2/r0D1=eW; d=4pr02n2=3e/r0; e = Vвкл/Vобр —объемная доля включений; Vобр = Sl; t=Dlt/l2.
Выражение (5.58) имеет достаточно сложный вид: оно содержит двойную сумму, причем для определения декрементов затухания необходимо решить трансцендентное уравнение. Поэтому для обработки результатов большее распространение получил метод моментов. Например, в методе проницаемости
tL =
m1 = T/6,
m2 = 7T2/180 + TT2K*/45 (1 + К*),
m3 = 31T3/2520 + 7 T2Т2К*/450 (1 + K*) + 2ТТ22К*/315(1 +К*),
где T=(1 + K*)l2/D1; T2=r02/D2; K*=ek.
Зная толщину мембраны и измерив три первых момента от кинетической кривой проницаемости, можно найти параметры D1, К* и T2. Для раздельного определения радиуса включения r0 и коэффициента диффузии в нем D2 какую-то из этих величин необходимо получить в отдельных экспериментах. Отметим, что в методе проницаемости значение первого момента не зависит ни от размеров, ни от геометрии включения. В формуле для второго момента геометрический фактор формально появляется, но играет роль константы k2 в рассмотренной ранее модели диффузии с обратимым захватом. Поэтому по первым двум моментам рассматриваемую модель невозможно отличить от модели диффузии с временным удержанием. Лишь высшие моменты зависят от формы включения. Для расчета D1 и D2 по методу моментов приходится использовать высшие моменты, отягощенные большими ошибками, либо проводить измерения на образцах различной толщины.
Аналогичный способ применим и для описания водородопроницаемости мембран, содержащих включения различной формы. Например, если включения представляют собой пластины толщиной l = 2h (цилиндры или призмы с непроницаемой боковой поверхностью), то
m1= T/6,
m2 = 7T2/180 + TТ2K*/9(1+K*),
m3 = 31T3/2520 + 7T2T2K*/90(1 + K*)+2TТ22 K*/15(1 + K*).
Если включения представляют собой цилиндры радиуса г„ с непроницаемыми торцами, то
m1= T/6,
m2 = 7T2/180 + TТ2K*/24(1+K*),
m3 = 31T3/2520 + 7T2T2K*/240(1 + K*)+2TТ22 K*/48(1 + K*).
Как следует из приведенных выражений, геометрическая форма включений играет роль, начиная со второго момента.
В сорбционном методе количество вещества, поглощенное пластиной, содержащей сферические включения, к моменту времени t равно
 |
(5.60) |
где mm=(2m+1)p/2.
Поток водорода из образца в десорбционном методе
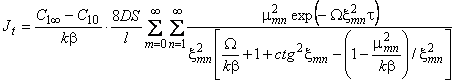 |
(5.61) |
Начальные моменты для кривых сорбции (или десорбции) [20]
m1= T/3+
T2K*/15(l + K*),
m2 = 42/15 + 4TT2K*/45(1
+ K*)+4T22 K*/315(1 + K*).
Из приведенных формул видно, что сорбционный и десорбционный методы более чувствительны к геометрической форме включения, чем метод проницаемости: параметры геометрической формы входят уже в формулы для первого момента.
До сих пор мы предполагали, что дефекты в ходе сорбции и проницаемости функционируют как стоки, улавливающие водород (рассмотренная выше модель справедлива только при условии D2<D1) и уменьшающие эффективный коэффициент диффузии. Между тем очевидно, что при D2<D1 (как это справедливо, например, для микропор) включения инородных фаз могут действовать не только как ловушки, но и как пути диффузии, увеличивающие скорость переноса через мембрану (за счет уменьшения эффективной толщины образца). Поэтому возникает необходимость разработки общей теории диффузии в дисперсионных средах. С этой целью сначала рассчитаем концентрационные профили водорода, возникающие при обтекании стационарным диффузионным потоком препятствий различной формы.
Пусть круглый бесконечный цилиндр (например, дислокация) радиуса r0 с коэффициентом диффузии D2 и константой растворимости L2 находится в бесконечной однородной среде с коэффициентом диффузии D1 и константой растворимости L1, через которую проходит стационарный диффузионный поток с плотностью потока J (ось цилиндра направлена перпендикулярно потоку). Решение будем искать в цилиндрической системе координат (r, j, z), записав уравнение Лапласа в виде
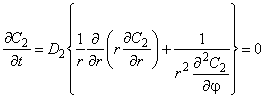 .
.
Используем условия на границе включения: С2 = KС1|r=rо, j=war (K=L2/L1) и D1(dC1/dr) = D2(dC2/dr) —и условия для вмещающей среды: С=-(Jr/D)cosj=Си (в бесконечности поле однородно) и С(0)=∞, где Си — концентрация водорода в «идеальной» среде с коэффициентом диффузии D1. Распределение концентрации в пространстве вне цилиндра: C1 = Cи(x) +C2*(r), внутри цилиндра: С2 = Си(х) +С2*(r), где С1* и С2* определяют искажающее действие включения.
В методе проницаемости Си(х) =С0(1—х/l).
Возмущение концентрации вне цилиндра
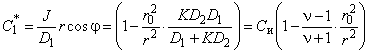 , , |
(5.62а) |
где n = P2/P1 = KD2/D1.
Возмущение концентрации внутри цилиндра
|
|
(5.62б) |
Если включение инородной фазы непроницаемо, то С1 = Си(1+r02/r2).
Из последнего выражения следует, что цилиндрическое включение сказывается (с точностью до 5%) на распределении концентрации до расстояния, в 2,25 раза превышающего его диаметр.
Аналогично для включения в форме шара уравнение
![]()
с граничными условиями на включении: C2 = KC1|r=r0;
Соответствующие возмущения концентраций
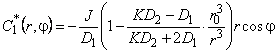 |
(5.63а) |
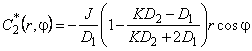 |
(5.63б) |
В методе проницаемости стационарное распределение концентрации водорода по толщине мембраны, содержащей отдельное включение в форме шара, центр которого располагается на глубине h от входной поверхности мембраны, определяется формулами
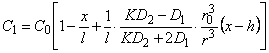 , , |
(5.64а) |
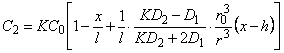 |
(5.64б) |
где r= (x2 + y2 + z2 + h2—2hx)1\2
Эти выражения используются при обработке результатов экспериментов по изучению диффузии трития в металлах, полученных методом продольного среза и техникой авторадиографии.
Введем понятие эффективного коэффициента диффузии в среде, представляющей собой дисперсию включений определенной формы в непрерывной матрице металла. Пусть размеры неоднородностей структуры значительно меньше толщины образца. На первом этапе рассмотрим разбавленные суспензии со случайным распределением дефектов, а затем перейдем к концентрированным и упорядоченным композитным материалам [21].
Для определенности сначала будем полагать, что включения имеют сферическую форму (радиус r0). При наличии локального равновесия на входе во включение стационарный поток через мембрану, содержащую дисперсию включений, определяется первым законом Фика, записанным в виде
|
|
(5.65) |
Тогда эффективный коэффициент диффузии
|
|
(5.66) |
с учетом уравнения (5.63б) имеем (см., например, [21])
|
|
(5.67) |
или
|
|
(5.68) |
Полученные выражения описывают диффузию в дисперсионных средах, содержащих включения различной формы. Действительно, a = 3/(2+n) для сфер, a = 2/(l+n) для цилиндров (перпендикулярных потоку); при параллельной диффузии аК=1 и nm=l+vФ2/Ф1; при последовательной диффузии (слойка) nm = n/(nФ1 + Ф2); при диффузии с обратимым захватом в ловушках nm=l/(l+ZKФ2/Ф1), где Z — координационное число, зависящее от типа кристаллической решетки; при диссоциативной диффузии (а=1) nm=(1+nФ2/Ф1)/(1+KФ2/Ф1).
Если включения имеют форму сфероидов с осями а0, b0, с0, (сфероиды распределены и ориентированы случайным образом),. то
|
|
(5.69) |
где
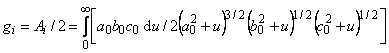 ;
;
| ga0+gb0+gc0=l. | (5.70) |
Из выражения (5.70) можно получить все приведенные выше формулы для различных типов гетерогенных сред. Для практических целей удобно использовать табл. 5.2.
Введение функции a(v) позволило нам в рамках единого подхода обобщить различные случаи диффузии в гетерогенных средах: параллельную диффузию по независимым каналам, диффузию с захватом в ловушках, диссоциативную диффузию, диффузию в среде, содержащей отдельные включения или дисперсию включений различной формы и ориентации, последовательную диффузию в слоистой среде и др. При соответствующем выборе функции а(n) можно найти эффективный коэффициент диффузии в неоднородной среде любого типа.
Таблица 5.2. Значения параметров геометрической формы в уравнении (5.70)
| Ai | Шар | Игла (вдоль потока) | Пластина (перпендик. потоку) | Цилиндр (перпендик. потоку) | Сфероид*) (a0, b0=c0) |
| А1 | 2/3 | 1 | 0 | 1 | Al' |
| А2 | 2/3 | 1 | 0 | 1 | A2' |
| А3 | 2/3 | 0 | 2 | 1 | Al' |
*) A1'=[(W—1/2 sin 2W/sin3W] cosW, где cos
W = a0/b0, а0<b0
A2'=(l/sin2W*) – 1/2 (cos2W*/sin3W*) ln [(l+sinW*)/(l - sinW*)], где cos
W* = b0/a0,
а0>D1 .
Если D1D2 (т. е. включение непроницаемо), то
nm=l/(l + aKФ2/Ф1),
тде а= 1,5 для сферических включений, а = 2 для цилиндрических, а = ∞ для пластин (слойка) и т. п. Для случая D1>>D2 (если К не слишком велико) известны асимптоты: nm@l-1,5КФ2/Ф1 для сфер, nm@l-2КФ2/Ф1 для цилиндров, nm@l-КФ2/Ф1 для игл, направленных вдоль потока (диссоциативная диффузия) и др.
Если D1>>D2 (поры) и К не слишком мало, асимптотой для сферических микропор будет nm@l+3КФ2/Ф1.
Приведенный выше подход можно легко обобщить на случай диффузии водорода в n-компонентной среде, каждая фаза которой характеризуется объемной долей Фi, коэффициентом диффузии Di, константой растворимости Li и параметром геометрической формы ai. Тогда
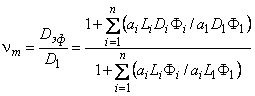 |
(5span lang="en-us">.71) |
где индекс 1 относится к компоненту, образующему сплошную фазу (т. е. фазу со значением ai=l).
Анализ приведенных выражений показывает, что при постоянной объемной концентрации включений инородных фаз эффективный коэффициент диффузии водорода не зависит от размеров включений и почти не зависит от их формы, когда разность между D1 и D2 не очень велика.
До сих пор мы рассматривали разбавленные суспензии (Ф2<<0,32 для сфер и Ф2<0,05для включений неправильной формы). Предпринимались неоднократные попытки получить удобные выражения для концентрированных дисперсий (см., например, [21]). Наибольший успех был достигнут при решении задачи диффузии через плотную упаковку включений.
Если включения представляют собой сферы одинакового диаметра, то эффективный коэффициент диффузии водорода будет зависеть от способа их упаковки (ограничимся случаем K=1):
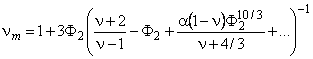 |
(5.72) |
тде a = 0,523 для простой кубической упаковки (формула (5.72) справедлива до Ф2<p/6@0,52); a = 0,129 для ОЦК-упаковки и a = 0,0752 для ГЦК-упаковки.
Аналогично для кубической решетки, составленной из цилиндров, параллельных друг другу и расположенных перпендикулярно к направлению потока
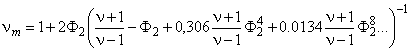 , , |
(5.73) |
где Ф2<p/4 = 0,785.
В общем случае решение задачи диффузии в «концентрированной» дисперсии (состоящей из кластеров случайным образом: распределенных включений произвольных формы и размера) представляет собой серьезную проблему. При больших значениях Ф2 уже нельзя полагать, что среда характеризуется коэффициентом диффузии D1 = Dи и средней концентрацией
![]() : включение вызывает аномальное распределение концентрации в непрерывной фазе (см., например, выражение (5.63а)), которое должно сказаться на эффективном коэффициенте диффузии. Для учета наложений друг на друга возмущений, создаваемых смежными включениями инородных фаз, можно воспользоваться методом усредненного поля, т. е. рассматривать задачу обтекания диффузионным потоком одиночного препятствия, находящегося в поле однородной концентрации
: включение вызывает аномальное распределение концентрации в непрерывной фазе (см., например, выражение (5.63а)), которое должно сказаться на эффективном коэффициенте диффузии. Для учета наложений друг на друга возмущений, создаваемых смежными включениями инородных фаз, можно воспользоваться методом усредненного поля, т. е. рассматривать задачу обтекания диффузионным потоком одиночного препятствия, находящегося в поле однородной концентрации
![]() со средним коэффициентом диффузии в окружающей среде
со средним коэффициентом диффузии в окружающей среде
![]() . Существуют различные способы введения
. Существуют различные способы введения
![]() и
и
![]() . В простейшем варианте формулы типа (5.68) сохраняют, но под
. В простейшем варианте формулы типа (5.68) сохраняют, но под
![]() понимают KD2/Dэф( где Dэф — эффективный коэффициент диффузии в среде, окружающей выделенное включение. Заменив ai(n) на
понимают KD2/Dэф( где Dэф — эффективный коэффициент диффузии в среде, окружающей выделенное включение. Заменив ai(n) на
![]() в формуле (5.71), найдем эффективный коэффициент диффузии Dэф в гетерогенной n-компонентной среде.
в формуле (5.71), найдем эффективный коэффициент диффузии Dэф в гетерогенной n-компонентной среде.
Если ввести
![]() и
и
![]() , то эффективный коэффициент диффузии среды, составленной из малых сфер, способных образовывать агрегаты, определится решением уравнения
, то эффективный коэффициент диффузии среды, составленной из малых сфер, способных образовывать агрегаты, определится решением уравнения
|
|
(5.74) |
т. е.
|
|
(5.74а) |
Аналогичное выражение получается и из теории перколяции.
Если среда представляет собой чередующиеся сферы с D1 и D2 то эффективный коэффициент диффузии определяется решением уравнения
|
|
(5.75) |
(В формулах (5.74), (5.75) мы полагали K=1.)
Отметим, что все подходы при D2<D1 дают совпадающие значения Dэф, но при D2>D1 (поры) введение различных приближений (и рассмотрение различных типов микроструктуры) приводит к существенным расхождениям в значениях Dэф. Особенно это заметно при переходе от одной непрерывной фазы к другой. Выражение (5.74а) можно рекомендовать для описания диффузии в сплавах, так как оно применимо для всего интервала значений Ф2: 0≤Ф2≤1.
Математический аппарат диффузии в дефектных средах позволяет установить ряд критериальных признаков данного класса моделей и сравнить их с имеющимися экспериментальными данными по диффузии водорода в металлах.
Проведенный выше анализ предсказывает высокую чувствительность растворимости и диффузии водорода к структурным неоднородностям материала. При этом параметры газопереноса должны отражать не столько свойства самого металла, сколько особенности микроструктуры, возникшие в ходе термической или механической обработки образца. Это обстоятельство, в свою очередь, может привести к сильному разбросу результатов измерений. Действительно, между данными различных авторов о поведении водорода даже в чистых металлах обнаруживаются существенные расхождения, далеко превосходящие ошибки экспериментальных исследований [1, 2, 22], особенно при пониженных температурах, где и ожидалось повышение активности ловушек.
Накопление газообразных примесей — одно из основных свойств ловушек — должно приводить к возникновению локальных неоднородностей в распределении водорода в дефектном металле. Прямые эксперименты, проведенные методом авторадиографии с использованием радиоактивного изотопа — трития — на металлах с различной атомной структурой (титан, никель, ниобий [23] и алюминий [24]), а также в сплавах на основе железа, никеля и особенно титана, подтвердили наличие тесной связи между тонкой структурой металла и картиной распределения водорода, атомы которого сегрегируют на дислокациях и субграницах зерен. В алюминии и некоторых других металлах водород концентрируется на границах зерен. Следует отметить, что не во всех металлах дефекты действуют как ловушки. Например, в таких металлах, как медь и палладий, скоплений водорода не наблюдалось.
Наличие процессов взаимодействия водорода с несовершенствами структуры металла, как правило (если не происходит облегченной диффузии по самим дефектам), приводит к уменьшению коэффициента диффузии. Эти следствия теории неоднократно подтверждались на практике (см., например, работы [1, 2, 14—16], в которых концентрацию ловушек изменяли с помощью термического отжига, зонной плавки, механической обработки, деформации, ионной бомбардировки, введением примесей замещения и т. п.).
Из теоретических предпосылок ожидали, что отношение количества водорода, находящегося в пластине при стационарном состоянии проницаемости Mпрон, к количеству водорода, находящемуся в том же образце при равномерном двустороннем насыщении Мсорб, должно находиться в интервале 0,5≤Mпрон/ Мсорб ≤0,85 в зависимости от величины С0, т. е. от парциального давления водорода. Эксперименты подтвердили эти предсказания [1].
Из феноменологической теории диффузии в дефектных средах следует, что если емкость диффузионных путей и ловушек неограниченна, то эффективные коэффициенты переноса не зависят от концентрации (т. е. от парциального давления на входе в образец) водорода. При ограниченной емкости ловушек (и/или диффузионных путей) эффективный коэффициент диффузии и константа растворимости зависят от концентрации водорода, причем эти зависимости близки к ступенчатой функции. В ряде работ подтверждена теоретически предсказанная асимметрия кривых сорбции и десорбции, а также кривых «прорыва» и «откачки» в методе проницаемости: скорость насыщения металлического образца водородом, как правило, выше скорости дегазации [13].
Часто полагают, что природу взаимодействия между атомами примеси и решеткой твердого тела лучше всего исследовать в области малых концентраций растворенного вещества, так как в этом случае можно пренебречь взаимодействием между атомами диффузанта. Однако если концентрация водорода настолько низка, что сравнима с концентрацией ловушек, то термодинамические измерения будут отражать не особенности взаимодействия примесных атомов с решеткой твердого тела, а особенности взаимодействия водорода с дефектами. Наиболее явно это проявляется в области низких температур, так как доля атомов растворенного вещества, взаимодействующих с дефектами решетки, увеличивается по мере уменьшения температуры.
Если растворимость примеси уменьшается с температурой, то предельная концентрация, начиная с которой термодинамическое поведение водорода определяется взаимодействием с дефектами, а не с решеткой, достигается еще скорее. В работе [25] продемонстрировано хорошее согласие этого следствия теории с экспериментом: если диффузия водорода в палладии (измеренная электрохимическим вариантом метода проницаемости) не зависит от концентрации водорода, то в деформированном на холоду на 50% палладии в интервале концентраций q=10-4 ÷10-5 (т. е. в условиях, когда q@Ф2) происходит резкое падение коэффициента диффузии.
Одним из следствий модели диффузии в дефектных средах является предсказание существования, помимо «ловушек», сильно уменьшающих Dэф, «антиловушек», способных увеличивать Dэф. Экспериментальную проверку этого утверждения проводили на примере диффузии водорода в палладии, легированном различными примесями замещения [26, 27]. Обнаружено, что если примеси Nb, Y и Ti сильно тормозят диффузию, то примеси Fe, Со, Mn, Сг и Ni не слишком значительно уменьшают скорость переноса. Еще слабее сказывается введение примеси Сu Dэф уменьшается при концентрации Сu 13 ат.%) и Ag (Ag практически не влияет на диффузию водорода в палладии вплоть до 25 ат.%). Аu начиная с 3 ат.% несколько увеличивает Dэф. Так как в меди, серебре и золоте энтальпия растворения много меньше (отрицательна), чем в чистом палладии, то благородные металлы в палладии играют роль «антиловушек».
В ряде случаев теория предсказывает отклонение формы кинетической кривой от «классической»: возможно появление эффектов «задержки» и эффектов достижения «псевдостационарных» или «псевдоравновесных» значений. Ожидается дрейф эффективного коэффициента диффузии во времени (при ранних временах Dэф мал, но затем постепенно увеличивается). Существуют экспериментальные подтверждения подобных эффектов [28]. Феноменологическое рассмотрение в рамках обсуждаемого класса моделей процесса десорбции позволяет объяснить тот факт, что в десорбционных экспериментах неоднократно наблюдалось падение потока газовыделения до фонового значения, несмотря на наличие в образце значительного количества водорода. Остаточный водород находится в ловушках и не принимает участия в диффузии. Лишь при повышении температуры ловушки начинают опустошаться, водород переходит в подвижную форму и выделяется из образца. При выходе на новую температурную ступеньку на кривой газовыделения наблюдается «пик-эффект», за которым следует медленное уменьшение скорости дегазации.
Вклад процессов захвата в общий процесс переноса зависит от толщины образца. При малых толщинах вероятность встречи атома водорода с ловушкой мала, аномалии, связанные с захватом, исчезают и кинетика диффузии определяется параметром Dэф = D (в этом состоит основное отличие данной модели от модели нелинейных граничных условий 3-го рода, когда отклонение от законов Фика усиливается как раз при малых толщинах); при очень больших толщинах кинетика диффузии описывается классическим уравнением, но с Dэф = D/ (1 + Кх); при промежуточных толщинах локальное равновесие установиться не успевает и форма кинетической кривой зависит от параметров k1 и k2.
Теория диффузии с захватом предсказывает возникновение изломов на аррениусовских зависимостях параметров диффузии, причем если число ловушек с ростом температуры не возрастает, то энергия активации, рассчитанная по низкотемпературному участку, будет выше полученной из высокотемпературных данных. Это положение получило экспериментальное подтверждение: значения коэффициентов диффузии во многих металлах при низких температурах намного ниже полученных экстраполяцией на эти температуры величин, измеренных при высоких температурах. Энергия активации процесса диффузии водорода в железе и сталях при низких температурах в 3—4 раза больше, чем при высоких.
Следует отметить, что не только наличие ловушек может приводить к появлению изломов на аррениусовских зависимостях. Такие же эффекты предсказывает модель диффузии, построенная с учетом физико-химических эффектов на границе раздела водород—металл, поскольку сопротивление поверхности образца, как и захват в ловушках, усиливается при низких температурах. Разграничение двух моделей удается провести путем сравнения данных по проницаемости из газовой фазы с данными по проницаемости, полученными электрохимическим методом. Так, в работе [29], проведенной на сверхчистом, хорошо отожженном в водороде a-железе, обнаружено четкое проявление граничных условий 3-го рода: высокотемпературный прямолинейный участок на аррениусовской зависимости коэффициента диффузии в случае электрохимического варианта (в котором процессы на поверхности мембраны не играют существенной роли) сохраняется до значительно более низких температур, чем в случае диффузии из газовой фазы. Однако характерный излом наблюдается и на кривых, свободных от сопротивления границы. Тем самым доказано, что даже в тщательно приготовленных образцах чистых металлов (особенно в железе) захват в ловушки все же имеет место и способен оказать влияние на процесс диффузии водорода.
В методе термодесорбционной спектроскопии кривые газовыделения могут иметь вид одиночного пика, параметры которого характеризуют свойства подвижной (если С10=1) или неподвижной ( при С20 = 1) фазы. Однако в общем случае кривые проявляют бимодальную форму: положение первого пика определяется энергией активации диффузии, положение второго — энергией выделения из ловушек. Если в твердом теле имеются ловушки различных типов или если на процессы дегазации накладываются твердофазные превращения (сопровождающиеся отжигом и возникновением дефектов), спектры термодесорбции принимают весьма сложную форму. Очевидно, что из обработки экспериментальных данных можно найти спектр заселенности дефектов.
Для расчета параметров спектра дефектов необходимо перед началом экспериментов по термически стимулированному газовыделению добиться полного заполнения водородом всех дефектов. Если дефекты образуют кластеры, способные вместить несколько атомов водорода (т. е. они могут образовывать комплексы типа HnVm), и если в металле существуют различные типы комплексов, то это неизбежно должно оказать влияние на структуру термодесорбционного спектра. Подобные эффекты экспериментально, наблюдались при изучении выделения дейтерия из молибдена [30].
Таким образом, к настоящему времени основные положения теории диффузии водорода в дефектных средах и ее следствия получили экспериментальные подтверждения. Очевидно, что адекватное описание кинетики и термодинамики переноса в реальных металлах может быть получено только с учетом процессов взаимодействия с несовершенствами структуры металла.
С другой стороны, явление диффузии может быть использовано как эффективный метод дефектоскопии металлов, поскольку позволяет определить плотность дефектов (и ее изменение при различного рода воздействиях), энергетические характеристики, размеры, емкость и заселенность их водородом. Направленные эксперименты по использованию водорода для дефектоскопии металлов следует проводить при низких температурах и малых концентрациях диффузанта.
Гельд П. В., Рябов Р. A., Кодес Е. С. //Водород и несовершенства структуры металла. М.: Металлургия. 1979. 221 с.
Верт Ч.//Водород в металлах. Т. 2. Прикладные аспекты/Под ред. Г. Алефельда, И. Фелькля. М.: Мир, 1981. С. 362—390.
Hurst D. G. CRRP-1124 //Atomic Energy of Canada, LTd, Chalk River; Ontario. 1962. Nov.
Gaus HJ //ZtsdiT. Naturforsch. A. 1965. Bd. 20. S. 1298—1308.
Barrer R. M.//J. Membrane Sci. 1984. Vol. 18. P. 25—35.
Bhatia D., Vieth W. R./llbid. 1980. Vol. 6. P. 351—357.
Yoshida M., Saito K. //Appl. Phys. 1967. Vol. 6. P. 573—681.
Попов E. В., Купряжкин А. Я., Рябов Р. А.//Журн. физ. химии. 1980. Т. 54, № 4. С. 1032—1034.
Купряжкин А. Я., Губанов В. A., Плетнев Р. Н., Швейкин Г. Я. //Дефекты и диффузия газов в кристаллах. Свердловск: УНЦ АН СССР, 1985. 220 с.
Бекман И. Н. //Радиохимия. 1983. Т. 25. С. 252—261.
Швыряев А. А. Диффузия родона в кристаллических полимерах: Автореф.дис. канд. хим. наук. М.: МГУ, 1982. 18 с.
McLellan R. S. //Acta met. 1979. Vol. 27. P. 1655—1963.
Бекман И. Н., Габис И. Е., Компаниец, Т. Н. и др. Исследование водородопроницаемости в технологии производства изделий электронной техники: Обзоры по электронной технике. М.: ЦНИИ «Электроника», 1985. 66 с. (Сер. Технология, организация пр-ва и оборудования; Вып. 1(1084)).
McNabb А., Foster P. К. //Trans Met. Soc. AIME. 1963. Vol. 227. P. 618 - 627.
Oriani R. A. //Acta met. 1970. Vol. 18. P. 147—157.
Robertson М. //Scr. met. 1981. Vol. 15. P. 137—139.
Yoshiara M., McLellan R. V. //Acta met. 1984. Vol. 30. P. 251.
Бекман И. Я.//Радиохимия. 1981. Т. 23. С. 281—287.
Ruckenstein E., Vaidyanatchan A. S., Younggust G. R. //Chem. Eng. Sci. 1971. Vol. 26. P. 1305—1318.
Волощук A. M., Золотарев П. П., Улин В. И. //Изв. АН СССР. Сер. 2. Химия. 1974. №6. С. 1250—1254.
Barrer R. M. //Diffusion in polymers/Ed. J. Crank, G. S. Park. L.; N. Y.: Acad. press, 1968. P. 165—180.
Volkl L, Alefeld G. Diffusion in solids: Resent development/Ed. A. S. Nowick, J. J. Burton. N. Y.: Acad. press, 1975. P. 231.
Бокштейн С. 3., Гинзбург С. С., Кишкин С. Т., Мороз П. М. Электронно-микроскопическая авторадиография в металловедении. М.: Металлургия, 1978. 264 с.
Foster L. M., Gillespie A. S., Jack Т. I., Hill M. W. //Nuckleonics. 1963. Vol. 21. P. 53—55.
McLellan R. V. //Scr. met. 1981. Vol. 15. P. 501.
McLellan R. V., Kircheim R.//J. Phys. Solids. 1980. Vol. 41. P. 1241.
McLellan R. V.//Scr. met. 1982. Vol. 16. P. 973.
Тажибаева И. Л., Бекман И. Н., Шестаков В. П., Руденко Н. В. //Физ. хим. механика материалов. 1985. Т. 21, № 1. С. 18—23.
Nagano M., Hagashi Y., Ohtani N. //Sct. met. 1982. Vol. 1. P. 973.
Городецкий А. Е., Захаров А. П., Шарапов В. M. //Журн. физ. химии. 1980. Т. 64, № И. С. 2874—2881.