Всес. конф. по теоретической и прикладной радиационной химии, г.Обнинск, октябрь 1984 г., "Наука", с.92
И.Н.Бекман,. И.Л.Тажибаева, А.Л.Гибрехтерман, Н.В.Руденко
Для установления роли плазменных возбуждений в механизме активации диффузии водорода в металлах низкоэнергетическим гамма-излучением, произведен учет вклада вторичных процессов при взаимодействии излучения с веществом на примере железа при Eg = 14 кэВ.
Известно, что основными процессами взаимодействия гамма-излучения с веществом являются: комптон-эффект, фото-эффект на К, L, M, N - оболочках, сопровождающийся оже-эффектом или вылетам характеристического фотона с последующими вторичными эффектами [I]. Задача решена о помощью разработанной в работе [2] программы на ЭВМ БЭСМ-6 (алгоритмический язык Фортран-Дубна). Моделирование траекторий вторичных электронов проводилось методом Монте-Карло по схеме индивидуальных соударений. Сечения элементарных процессов взаимодействия электронов с веществом вычислялись по разработанным программам [3, 4]. Сечения находятся из решения системы дираковских уравнений численным методом для частиц со спином. При суммировании фаз применялась процедура ускорения сходимости рядов. В качестве экранированного потенциала выбран потенциал модели независимых частиц. Для расчетов использовались табличные значения атомных характеристик вещества мишени. Были рассмотрены упругие и неупругие соударения вторичных электронов с атомами мишени. Сечения упругого рассеяния вычислялись методом парциальных фаз с потенциалом независимых частиц [З]. Неупругие процессы включают в себя электрон-электронное рассеяние, плазменное возбуждение и ионизацию К, L, M , N... оболочек атома. В алгоритме отдельно рассматриваются взаимодействия на валентных и оболочечных электронах атома. Сечения рассеяния на валентных и свободных электронах (электрон-дырочные и плазменные возбуждения) описываются с помощью модели комплексной диэлектрической постоянной [5, 6]. Сечение ионизации К, L, M , N... оболочек вычисляются на основе классической модели бинарных соударений [7].
Траектории вторичных электронов, включая оже-, и d -электроны, последовательно прослеживаются от соударения к соударению. Расстояния между последовательными актами взаимодействия рассматриваются с учетом экспоненциальной зависимости ослабления излучения. Для неупругого взаимодействия рассчитываются потери энергии и угол рассеяния. При упругом взаимодействии вычисляется только угол рассеяния. Траектория частицы прослеживается до ее практически полного поглощения (остановки) веществом. При Еg = 14 кэВ толщина слоя ослабления в 10 раз составляет в железе 100 мкм.
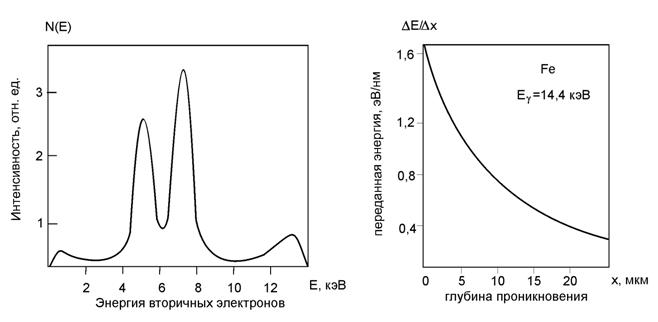
Данная модель позволяет получать все основные характеристики прохождения гамма-квантов и вторичных электронов через вещество: распределение поглощенной энергии, энергоугловые распределения отраженных электронов, коэффициенты пропускания и обратного рассеяния, распределение максимальной глубины проникновения и количества столкновений для отраженных электронов. В модели не учитывается электрон-фононное взаимодействие, распределение по скоростям оболочечных электронов и эффекты обмена при рассеянии. Энергетический спектр вторичных электронов от Еg = 14 кэВ в железе приведен на рис.1.
Таким образом, для качественного объяснения увеличения диффузионной подвижности водорода в металле с помощью машинного моделирования прохождения низкоэнергетического гамма-излучения проведено рассмотрение генерации потока вторичных электронов (фото-; комптон-, оже-) в железе при Еg=14,4 кэВ и их воздействие на вещество мишени и диффузант.
Феноменологический подход к объяснению механизма радиационно-стимулированной диффузии водорода в металлах дал основание предположить возникновение под действием низкоэнергетического гамма-излучения второго канала междоузельной диффузии с меньшей энергией активации. Полученные результаты по увеличению диффузионной подвижности водорода свидетельствуют о высокой эффективности воздействия низкоэнергетического гамма-излучения на элементарный акт диффузии [8]. Наблюдаемые эффекты могут быть объяснены только коллективными процессами: возникновением фононных колебаний или генерацией плазмонов. Дополнительное количество фононов путем электрон-фононного взаимодействия может, например, изменить уровень Ферми в металле. Доминирующим процессом замедления электронов в рассматриваемом диапазоне энергии является возбуждение объемных плазмонов размером 15 нм и временем жизни @10-16 с [9]. Одним из факторов, влияющих на увеличение подвижности междоузельного атома, может явиться вырывание примеси из потенциальной ямы при распаде на ней электронных возбуждений, сопровождающееся уменьшением и даже снятием ее диффузионного барьера. Коэффициент диффузии заряженной примеси в значительной степени также зависит от состояния электронного газа в металле. Вероятность рассеяния плазмонов на связанном (локализованном) электроне атома водорода, вероятно, выше, чем на валентных электронах металла. Так как плазмон имеет довольно большую протяженность и объем, то естественным будет предположение о большей эффективности взаимодействия плазменных возбуждений с атомом водорода, чем непосредственная передача энергии вторичных электронов водороду в решетке металла. Поэтому взаимодействие плазменных колебаний с примесью внедрения за счет обобществления электрона атома водорода с электронами металла и участия его в коллективных колебаниях электронного газа металла, может изменить и эффективный заряд, и радиус водорода. Это должно привести к увеличению эффективного коэффициента диффузии за счет открытия нового облегченного канала и, возможно, надбарьерной диффузии. Для функционирования такого механизма необходимо существование непрерывной области возбуждения электронной подсистемы металла.
Машинным моделированием по программе [2] было вычислено распределение энергии вторичных электронов, переданной веществу мишени в плазменных колебаниях. Эта выделившаяся энергия в образце железа при Еg = 14 кэВ на плазменные возбуждения в зависимости от глубины проникновения вторичных электронов и в пересчете на один падающий фотон представлена на рис.2.

|
Рис.1. Энергетический спектр вторичных электронов от Еg=14 кэВ в образце железа. |
Рис. 2. Распределение энергии, переданной веществу в плазменных колебаниях, в зависимости от глубины проникновения. |
Расчеты проводились по глубине мишени на выбранныx участках, равных 2 мкм. На данных интервалах подучено равномерное распределение выделившейся энергии, перешедшей в плазменные возбуждения. По толщине образца количество выделившейся энергии на плазменные возбуждения убывает экспоненциально согласно закону ослабления излучения. Получено, что на один падающий гамма-квант возникает в единицу времени 1,5 объемных плазмона, а с учетом всех вторичных процессов (оже-, d- и вторичных электронов) и их статистического характера распределения, это количество становится порядка 10. Энергия вторичных электронов при фотоэффекте на К, L- оболочках равна соответственно, 7 и 13 кэВ, оже- электронов I кэВ. Электрон с энергией 10 кэВ проходит путь до полной остановки, равный 3000 Ǻ. Пробег электрона до образования плазмона согласно формуле Феррелла [10] составляет 160 Ǻ. Время жизни плазмона сравнимо по порядку величины с временем жизни электрона с E0 = 10 кэВ и равно 10-16 с. За это время жизни плазмон успевает пройти расстояние 100 Ǻ. Тогда объем зоны действия плазмона равен 107 Ǻ. Следовательно, в момент рождения второго плазмона одним вторичным электроном первый плазмон все еще существует. Это приводит к непрерывному пространственно-временному распределению плазменных возбуждений. При концентрации водорода, равной 1018 ат/см3 в зоне действия плазмона, рожденного одним вторичным электроном в металле, оказывается до 100 атомов водорода. Полученные результаты свидетельствуют о возможности существования дополнительного плазмонного канала диффузии водорода в металле при воздействии гамма-излучением допороговых энергий. Более детальное рассмотрение этого вопроса требует учета вклада фононных колебаний, возникающих при затухании плазмонов в металле, т.е. плазмон-эдектрон-фононных взаимодействий в системе водород-металл.