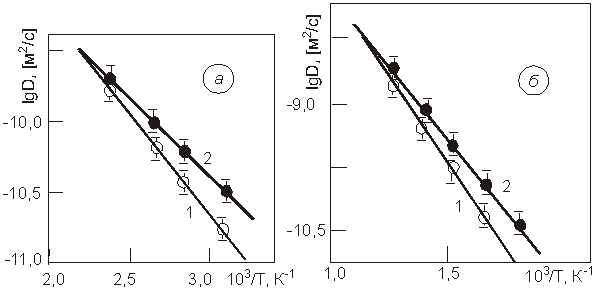
 Рис. 1. Температурная
зависимость коэффициентов диффузии водорода в палладии (а) и в никеле (б): 1 —
без облучения; 2 — при облучении.
Рис. 1. Температурная
зависимость коэффициентов диффузии водорода в палладии (а) и в никеле (б): 1 —
без облучения; 2 — при облучении.Физико-химическая механика материалов, 1-1985, с.18-23
УДК 533.15:5,19.219.3
И.Л. Тажибаева, И.Н. Бекман, В.П. Шестаков, Н.В. Руденко
Цель данной работы — определение коэффициентов диффузии, констант проницаемости и растворимости водорода в палладии, никеле и армко-железе под воздействием низкоэнергетического гамма-излучения [I].
 Рис. 1. Температурная
зависимость коэффициентов диффузии водорода в палладии (а) и в никеле (б): 1 —
без облучения; 2 — при облучении.
Рис. 1. Температурная
зависимость коэффициентов диффузии водорода в палладии (а) и в никеле (б): 1 —
без облучения; 2 — при облучении.
Установлено (риc. 1а, б, кривые 1), что без облучения все кинетические кривые диффузии водорода в палладии и никеле хорошо спрямляются в функциональном масштабе, проницаемость прямо пропорциональна толщине образца и корню квадратному от входного давления водорода, кривые «прорыва» и «откачки» совпадают друг с другом, аррениусовские зависимости всех параметров носят линейный характер. В армко-железе при этом наблюдаются некоторые отклонения (рис. 2): кинетическая кривая проницаемости в функциональном масштабе имеет излом, эффективный коэффициент диффузии уменьшается с увеличением толщины образца, кривые «прорыв»—«откачка» не совпадают (десорбция медленнее сорбции, на аррениусовской зависимости коэффициентов диффузии наблюдается излом, энергия активации при низких температурах выше, чем при высоких). Аномалии усиливаются с ростом толщины мембраны.
Рис. 2. Температурная зависимость коэффициентов диффузии водорода и
армко-железе: 1- без облучения; 2 - источник 57Со с фильтром; А —
источник 57Со, А=1·108 Бк; 4 — источник 57Со,
=2·108
Бк.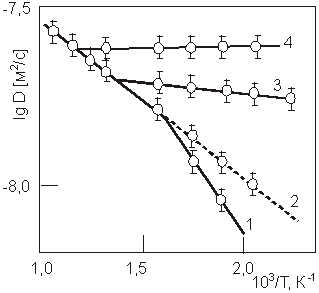
Перечисленные факты полностью соответствуют критериальным признакам модели диффузии в дефектных средах. При высоких температурах проникновение водорода в a-железе соответствует классическим законам диффузии, что позволяет рассчитать параметры междоузельной диффузии (табл. 1) и аррениусовской зависимости (табл. 2). Энергия активации диффузии ED=8,3 кДж/моль, теплота растворения dH=33,44 кДж/моль. При низких температурах ED =14,1 кДж/моль, dH=9,18 кДж/моль. Результаты, полученные при испытаниях в низкотемпературной области, обрабатывали в рамках теории диффузии в дефектных средах (модель Херста — Гаусса) [2]. Предполагали, что диффузионная среда локально-неоднородная (точечные дефекты, микропоры, включения инородных фаз). Ловушки захватывают мигрирующий атом и yа некоторое время выводят его из диффузионного процесса. Если константы скорости реакции захвата атома водорода ловушкой K1 и скорости освобождения из ловушки Κ2, а также число ловушек значительно больше концентрации водорода, то диффузия при наличии обратимой химической реакции первого порядка описывается следующими уравнениями:
|
|
(1) |
где С и m — концентрации водорода в диффузионных путях и ловушках соответственно. Если K1C= K2m, константа равновесия реакции захвата
|
Kx=m/C=K1/K2=K(N2/N1), |
(2) |
где
|
K=l1/l2=exp(EK/RT), |
(3) |
l1,
l2 — вероятность входа
и выхода атома диффузанта в ловушку соответственно; N1 — число
диффузионных путей; Ν2 число ловушек;
EК
= Ek1-Еk2, где
Ek1 — глубина ловушки.
Введем понятие эффективного коэффициента диффузии:
|
|
(4) |
С ростом температуры эффективная энергия активации уменьшается. Растворимость в дефектном материале выше, чем в «идеальном», т. е.
|
Сs эф. = Cs ид (1+Kх). |
(5) |
| Параметры диффузии |
Элемент | ||
|
Pd (320 К) |
Ni (570 К) |
Fe (470 K) | |
| D, м2/с | (2,78±0,33)·10-11 | (0,65±0,06)·10-10 | (0,628±0,072)·10-8 |
| Dэфф, м2/с | (5,32±0.59)·10-11 | (1,22±0,09)·10-10 | (2,83±0.28)·10-8 |
| Dg/D | 1.91 | 1,86 | 4,5 |
| P, моль/(м·с·Па1/2) | (1,34±0,12)·10-9 | (2,91±.0.30)·10-12 | (0.52 ± 0.05)·10-10 |
| Рgэф, моль/(м·с·Па1/2) | (2,03±0,17)·10-9 | (4,83±0,50)·10-12 | (0,50±0,00)·10-10 |
| Рg/P | 1,51 | 1,05 | 1.0 |
| Сs, моль/(м3·Па1/2) | (347±36)·10-6 | (0.31±0,03)·10-6 | (5.92±0,62)·10-8 |
| Сsgэф, моль/(м3·Па1/2) | (273±29)·10-6 | (0,28±0,03)·10-6 | (1,81±0,19)·10-8 |
| Сsg/Сs | 1,27 | 1,1 | 3,3 |
Значения «истинных» коэффициентов диффузии D и константы растворимости Сs находим путем экстраполяции соответствующих зависимостей от высоких температур:
| EDэф (T) = ED + [Kx(T)/ Kx(T)+1] Еk. |
(6) |
Вычислив из уравнения (2) соотношение N2/N1, рассчитываем концентрацию дефектов при различных температурах N2(T) (или объемную долю включений F2=N2/N, где N=N1+N2). Далее определяем заселенность ловушек q=Cs/N2. Окончательное значение констант K1 и K2 находим нелинейным методом наименьших квадратов по специально разработанной программе, реализованной на ЭВМ БЭСМ-6. Имея параметры K1 и K2, находим глубину ловушки Ek, и ее размер:
|
F2=V2/V0=VДN2/V0 |
(7) |
где V0 - объем образца: VД- объем дефекта. Считая дефект сферически симметричным, вычисляем его радиус rД= 2·10-8 см.
| Mеталл | D01 | ED1 | D02 | ED2 | ED2/ ED1 | Ek1 | Ek2 |
| Pd | 1,5·10-7 | 23,1 | 2,9·10-6 | 15,1 | 1,53 | — | -33,9 |
| Ni | 5,9·10-6 | 44,8 | 2,39·10-6 | 15,3 | 2,92 | — | -9,97 |
| Fe | 2,24·10-7 | 14,3 | 1,36·10-7 | 0,2 | 71,5 | -28,5 | -28,9 |
| Fe(gф) | 2,24·10-7 | 14,3 | 2,86·10-7 | 1,13 | 12,7 | -28,5 | -18,4 |
Примечание. gф — источник 57Со с фильтром; ED, ЕК — кДж/моль.
Таким образом, использование диффузионных данных позволяет рассчитать плотность ловушек, глубину и заселенность их при различных температурах, а также геометрические размеры (табл. 3). Так, в случае армко-железа мы имеем дело с точечными дефектами, плотность которых достаточно велика: при температуре 470 К. N2 = 4,3·1020 л/см3, что соответствует 0,17 об. %. Для хорошо отожженного железа N2=2·1019 л/см3 или 0,01 об. %, однако в обычном железе в сталях число ловушек может повышаться до N2=1021 л/см3 [3]. Энергия активации взаимодействия водорода с ловушкой Еk= -28,5 кДж/моль, глубина ловушки Ek2=20,1 кДж/моль. Число ловушек с ростом температуры практически не изменяется, что свидетельствует об их неравновесной природе. Заселенность ловушек невелика (q = 4·10-3), это подтверждает справедливость допущения об неисчерпаемости ловушек в процессе диффузии и, следовательно, правильность выбора системы (1) для ее описания.
| t, K | Kх | K | Ф2·10-3, % | N2·1020 л/см3 | q2·Ι0-2 | Cs·Ι016 ат/см3 |
| 470 | 2,27 | Ι423 | 1,69 | 4,16 | 3,82 | 1,59 |
| 520 | 1,04 | 711 | 1,46 | 3,80 | 4,84 | 1,84 |
| 570 | 0,79 | 401 | 1,97 | 5,12 | 4,79 | 2,45 |
| 620 | 0,40 | 248 | 1,61 | 4,19 | 6,37 | 2,67 |
При воздействии гамма-излучения на проникновение водорода сквозь палладий и никель наблюдается увеличение эффективного коэффициента диффузии, уменьшение эффективной константы растворимости и некоторое возрастание величины стационарного потока (меньшее, чем ожидалось по изменению коэффициента диффузии). Все кинетические кривые хорошо спрямлялись в функциональном масштабе. Влияние низкоэнергетического гамма-излучения усиливается с уменьшением температуры, увеличением активности источника и входного давления водорода. Максимальный эффект зафиксирован при облучении источником 57Со активностью 2·108 Бк. Таким образом, можно заключить, что облучение снижает энергию активации диффузии водорода в палладии от 23,1 до 17,2 кДж/моль, а в никеле — от 44,8 до 40,2 кДж/моль.
Увеличение эффективного коэффициента диффузии можно объяснить появлением в результате радиации второго диффузионного канала со своими коэффициентом диффузии и константой растворимости. С целью описания кинетики переноса используем модель диссоциативной диффузии [4], предполагающей ее протекание по двум каналам, между которыми происходят процессы взаимного обмена. Исходную систему уравнений можно записать в виде:
|
|
(8) |
где С1 — концентрация водорода в первом диффузионном канале (обычная диффузия по междоузлиям); С2 — концентрация водорода но втором канале, возникшем в процессе облучения; K1' = l1'N2' —константа скорости процесса перехода из первого канала во второй; l1'— вероятность этого перехода; N2'— число потенциальных ям второго типа; K2' = l2'N1' и l2' — соответствующие параметры обратного перехода; N1' — число потенциальных ям первого типа; D1 — коэффициент обычной диффузии; D2 — коэффициент диффузии по второму каналу. Допустим существование равновесия K1'C2= K2'C2. Тогда систему (8) можно представить так:
|
Dg эф = (D2 K2'+ D1 K2')/( K1'+ K2'). |
(9) |
Константа равновесия реакции обмена между двумя каналами следующая:
|
K=K1'/ K2'=C2/C1=K0exp[-Ek'/(RT)] |
(10) |
где Ek'= Ek1'- Ek2' — энергия активации процесса обмена между двумя каналами. С учетом температурной зависимости, имеем:
|
|
(11) |
где A0 = K0D02, ED1, и ED2— энергии активации диффузии по первому и второму каналу. Для оценки параметров диффузии по образовавшемуся каналу находим константу равновесия
|
|
(12) |
и параметры ее температурной зависимости К0 и Еk. Используя эти данные, и определенные ранее параметры D02 и ED2 определяем значения D01 и ED1. Преобразуя формулу (10) к виду
|
|
(13) |
находим относительную плотность вновь образовавшихся путей:
|
|
(14) |
где l1'/l2' = exp[-(ED1- ED2)/(RT)] (табл. 4).
| Т, К | D1·10-11 | D2·10-11 | D2/ D1 | K | t1/t2 | F2 | Φ2/Φ1 |
|
Pd | |||||||
| 320 | 2,78 | 14,7 | 5,29 | 0,27 | 0,05 | 0,84 | 5,25 |
| 350 | 5,03 | 32,1 | 6,38 | 0,22 | 0,07 | 0,77 | 3,35 |
| 370 | 8,89 | 55,4 | 6.23 | 0,07 | 0,08 | 0,48 | 0,92 |
| 420 | 20,5 | 72,3 | 3,57 | 0,05 | 0,10 | 0,33 | 0,49 |
|
Ni | |||||||
| 570 | 6,56 | 63,4 | 9,66 | 0.11 | 0,02 | 0,86 | 5,6 |
| 620 | 23,9 | 103,0 | 7,62 | 0,13 | 0,03 | 0,80 | 4,0 |
| 650 | 26,6 | 182,0 | 3.83 | 0,15 | 0,04 | 0,75 | 3,0 |
| 720 | 102,0 | 339,0 | 3,32 | 0,17 | 0,07 | 0,22 | 2,8 |
| 770 | 175,0 | 535,0 | 3,06 | 0,02 | 0,09 | 0,17 | 0,2 |
|
Fe (без фильтра) |
Fe (с фильтром) | ||||||||||
| Т, К | D1·10-8 | D2·10-8 | D2/ D1 | K | ;t1/t2 | F2 | D2·10-8 | D2/ D1 | K | t1/t2 | F2 |
| 470 | 0,628 | 8,19 | 13,04 | 3.52 | 0.04 | 0.99 | 1,33 | 2,12 | 0.52 | 0,48 | 0,52 |
| 520 | 0,853 | 5,60 | 6,57 | 1,33 | 0.06 | 0,96 | 2,08 | 2,44 | 0,43 | 0,54 | 0,44 |
| 570 | 1,12 | 5,20 | 4,65 | 0,8 | 0,07 | 0,91 | 2,11 | 1,88 | 0,23 | 0,55 | 0,29 |
| 620 | 1,56 | 8.87 | 5,69 | 0,62 | 0,09 | 0,87 | — | — | — | — | — |
| 670 | 1,82 | 9,54 | 5,24 | 0,46 | 0,11 | 0,81 | — | — | — | — | — |
Следовательно, под действием облучения низкоэнергетическими гамма-квантами в палладии и никеле появляются облегченные пути диффузии, характеризующиеся повышенным коэффициентом диффузии и пониженной константой растворимости. Образованный канал интенсивно функционирует при низких температурах, а при повышенных его роль ослабевает. Отметим, что при низких температурах почти все исходные диффузионные пути переходят в новое возбужденное состояние.
Исследованиями установлено, что низкоэнергетическое гамма-излучение более эффективно в случае диффузии водорода в a-Fe, нежели в Pd и Ni (см. табл. 1 и рис. 2). Так, облучение энергией 0,122 МэВ от источника 57Со (линию 0.014 МэВ удаляли специальным фильтром) изменяет механизм диффузии: диффузия с захватом переходит в классическую диффузию, изломы на кинетических кривых, построенных в функциональном масштабе, исчезают, температурная зависимости параметров подчиняется аррениусовской зависимости, кривые «прорыв» — «откачка» совпадают друг с другом, эффективные энергии активации равны таковым для бездефектного железа. Изменение характера облучения ускоряет диффузию водорода в железе, что свидетельствует о появлении второго облегченного капала диффузии. Аналогичен процесс диффузии водорода в палладии и никеле. Этот случай диссоциативной диффузии можно представить следующей системой уравнений:
|
|
(15) |
где K1" — константа скорости выделения водорода из нормального междоузлия в возникшее при облучении (с меньшей глубиной залегания водорода) и в ловушку; K2" — константа перехода из возбужденного (нового) междоузлия в нормальное и в ловушку; К3"— константа выхода из ловушки в первый и второй каналы; С1, С2, m — концентрации водорода в первом, втором каналах и ловушках соответственно. Система (15) описывает параллельную диффузию по двум термодинамически равновесным каналам. Атомы водорода могут попадать в ловушку как из обычного капала диффузии, так и из образовавшегося под действием радиации. Коэффициенты D2, K1", K2", K3" зависят от, энергии и плотности потока излучения. Процессы обмена описываются кинетикой обратимой химической реакции первого порядка. При условии К1"С1+ К2"С2= 2К3"m можно ввести константы равновесия соответствующих реакций:
|
K1=2K1"/K2", K2=2K1"/K3". |
(16) |
Эффективный коэффициент диффузии в данном случае следующий:
|
Dэф = (D1 + К1 D2)/(1 + К1 + К2). |
(17) |
Из полученных формул вытекает, что образование ловушек приводит к уменьшению эффективного коэффициента диффузии, а появление дополнительного канала — к его увеличению. Под воздействием радиации константа захвата уменьшается, а константа перехода в возбужденный канал — возрастает и, следовательно, увеличивается коэффициент диффузии, исчезают различного рода аномалии и при больших дозах возможна диффузия по одному облегченному каналу.