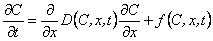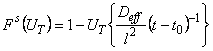Thermochimica Acta, 190 (1991) 1-13
Elsevier Science Publishers B.V., Amsterdam
INERT GAS DIFFUSION PROBE OF POLYMER MATERIALS
Igor N. Beckman
Department of Radiochemistry, Moscow Slate University, 199234 Moscow (USSR)
Abstract
Inert radioactive gases were used as probes for investigating the microstructure changes that occur in solids as a consequence of chemical and physical processes. The measurement of the inert-gas release from solids during thermal treatment is the principle of emanation thermal analysis. The application of this method to a number of inorganic materials has been described by Professor Balek. The application of inert gas probes in the diagnostics of polymer materials is described.
INTRODUCTION
A large number of experimental techniques exist that are suitable for the investigation of the texture and morphology changes that occur in polymeric materials. The methods are based on, for example, the measurement of mechanical properties, thermal properties (calorimetry), adsorption and desorption of gases, and gas permeability measurements. The radioactive tracer techniques used so far make it possible to investigate the diffusion properties of the polymers, to locate structure irregularities and defects and to locate the defects using autoradiography, etc.
Inert radioactive gases provide a valuable tool for investigating polymers during for example, mechanical, radiation and other treatments that influence the microstructure of the polymers and for investigating the diagnostics of polymer membranes during their operation.
Radioactive tracers have been used for more than 30 years at the Department of Radiochemistry, Moscow State University, USSR, under the guidance of Professor K.B. Zaborenko [1] in the study of various solid-state processes, including those that occur in polymers [2]. The present author met Professor Balek for the first time in 1964, as a postgraduate student. Since then, Professor Balek has created a scientific school in Czechoslovakia which has succeeded in developing emanation thermal analysis and in finding new fields of application for this method. The method and its numerous applications are described in Professor Balek's book "Emanation Thermal Analysis and other Radiometric Methods" [3].
In this paper the potential of the inert-gas diffusion probe in the diagnostics of polymers and the computer evaluation of experimental results are described.
DIAGNOSTICS OF GAS POLYMER SEPARATION MEMBRANES USING AN INERT-GAS DIFFUSION PROBE
The inert-gas-probe technique described in this paper is based on the measurement of the radioactive inert gases that pass through a membrane. Various inert gases, e.g. radionuclides of
133Xe, 85Kr and 222Rn have been used [4,5]. The application of this technique consists of inserting trace amounts of radioactive inert gas at the input of the membrane placed in standard equipment [5]. Several techniques involving the application of inert-gas probes have been used for the diagnostics of polymer membranes. These techniques and their applications are described below.
Gas permeability methods
A trace amount of the inert radioactive gas is inserted at the membrane input and the amount of inert gas passing through the membrane is measured continuously over time (see Fig. l(a)) or the change in the inert-gas flow through the membrane is measured (see Fig. l(b)).
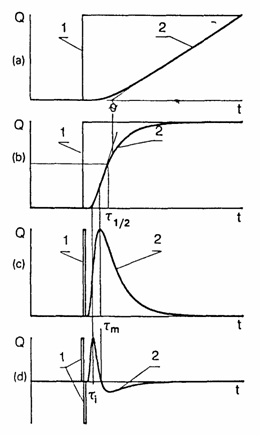 Fig. 1. Typical experimental curves resulting from various gas permeation methods. Curves 1 and 2 correspond to the time dependences of the partial pressure of the diffusion agent on the membrane input and that of the gas flux through the membrane, respectively, (a) Integral method: (b) differential method; (c) impulse method; (d) differential impulse method.
Fig. 1. Typical experimental curves resulting from various gas permeation methods. Curves 1 and 2 correspond to the time dependences of the partial pressure of the diffusion agent on the membrane input and that of the gas flux through the membrane, respectively, (a) Integral method: (b) differential method; (c) impulse method; (d) differential impulse method.
Gas permeability method with autoradiographic detection [4]
A trace amount of the inert radioactive gas is inserted at the membrane input and, after establishing a steady state inert-gas flow, the diffusion process is stopped by freezing and the membrane is put in between two photographic plates to obtain autoradiographs. A map of the inert-gas distribution obtained in this way at the output of a polypropylene membrane is shown in Fig. 2. The differences between the maps obtained at the membrane input and output, the spectra of the local diffusion coefficients and solubility constants of the inert gas in the" membrane material can be determined (see Fig. 2(b)). From the spectra in Fig. 2(b) we have concluded that the temperature treatment of the membrane in the air at 80-100�C led to an increased appearance of higher values of the diffusion coefficient D, probably due to the development of microcracks.
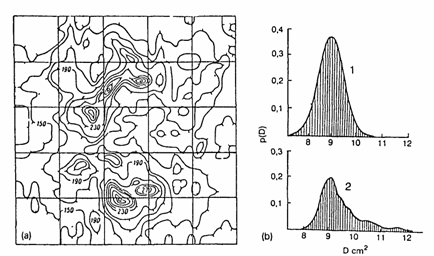
Fig. 2. Diagnostics of a polypropylene membrane (thermally treated at 80-100�C) by means of a
222Rn diffusion probe, (a) Map of the 222Rn distribution in the polymer membrane constructed on the basis of autoradiography results, (b) Spectra of local diffusion coefficients of
222Rn in the virgin membrane (curve 1) and the thermally treated membrane (curve 2).
Pulse method for the gas permeability measurement [5,6]
This is based on the measurement of the inert-gas concentration pulse passed through the membrane (see Fig. l(c)). The gas is inserted in the form of an infinitely thin pulse at the membrane input, and the time T required to attain the maximum flux at the membrane output is determined. The appearance of a deviation in tfrom the standard value tst (can be considered as a signal of damage to the membrane separator. The results obtained with this method in the investigation of polyvinyltrimethylsilane are shown in Fig. 3.
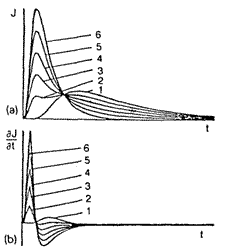
Fig. 3. Results obtained with the pulse method of gas permeability measurement for the polyvinylirimethylsilane membrane, (a) Response to an infinitely thin pulse of
85Kr; (b) response to the differential pulse of 85Kr. Curves: (1) the membrane in the perfect (undamaged) virgin state; (2-6) membranes with developing microcracks.
Differential inert-gas-pulse method
This is based on the interruption of the steady flow of the inert gas, creating a series of subsequent pulses which are inserted at the membrane input (Fig. l(d)). The response curves obtained at the polyvinyltrimethylsilane membrane output are demonstrated in Fig. 3.
Double-pulse method for gas permeability measurement
Two subsequent radioactive inert-gas rectangular pulses are inserted at the input of the membrane (the time interval between the pulses being equal to their widths) and the passage of the double pulse at the output response is measured (see Fig. 4). The single-peak response curve (curve 1, Fig. 4) corresponds to the perfect state of the membrane. Splitting of the single peak into a double peak (curves 2-6, Fig. 4) indicates the appearance of microcracks in the membrane.
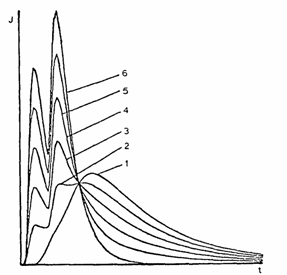
Fig. 4. Results of the double-pulse method using a
85Kr diffusion probe. Curves: (1) the membrane in the perfect (undamaged) virgin state; (2-6) membranes with developing microcracks.
Using the above techniques the quality and operation properties of the membranes can be investigated continuously over the course of the operation of the membrane. The heights and widths of the gas pulses and the type of inert gas used as the, diffusion probe can be varied during the defectoscopic investigation of the membrane. Even a mixture of inert gases can be used as a probe of the defect state of the material.
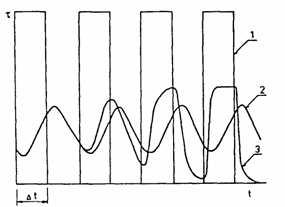 Fig. 5. Experimental results of the inert gas probe method using a set of rectangular pulses of
222Rn. Curves: (1) value of the inert gas concentration at the membrane input; (2 and 3) changes in the inert-gas flux at the membrane output in the case of a stable and unstable membrane, respectively.
Fig. 5. Experimental results of the inert gas probe method using a set of rectangular pulses of
222Rn. Curves: (1) value of the inert gas concentration at the membrane input; (2 and 3) changes in the inert-gas flux at the membrane output in the case of a stable and unstable membrane, respectively.
The results of the application of an inert-gas probe in the investigation of the changes in a polymer material are demonstrated in Fig. 5. Curve 1 represents the original pluses of the inert gas (222Rn) and curves 2 and 3 represent the distorted pulses of the gas after its passage through a stable or unstable polymer membrane [5], respectively.
EVALUATION OF INERT-GAS DIFFUSION PROBE RESULTS
Using computers it was possible to collect and store all the experimental data obtained with the methods applied, to construct a theoretical model of diffusion, and to evaluate the diffusion parameters of the polymer material. We have prepared a set of computer programs called DIGS (diffusion of inert gases in solids) for the statistical treatment and interpretation of the results of various methods used to investigate the transport properties of polymer materials.
A bank of general diffusion models has been organized on the basis of both analytical and numerical solutions of diffusion cases. In the bank of experimental information the standard interface for the input of experimental data is used.
The set of programs involves four parts, which can be used for: (i) the preliminary treatment of experimental results; (ii) the evaluation of results on the basis of the classical diffusion model; (iii) choosing the most suitable phenomenological diffusion model (in cases where the classical diffusion model is inadequate); and (iv) choosing a suitable physical diffusion model.
Preliminary treatment of experimental results
One of the main tasks of this part of the program is to eliminate apparatus errors. Unfortunately, in the course of the registration of the diffusion flux in the experimental measuring system a distortion of the input signal occurs due to the integration effect of the detector used and to the inertia of the apparatus caused by adsorption of the penetrating agent on the walls of the apparatus, etc.
Consequently, in real experiments, especially when using so-called rapid membranes which are characterized by a high diffusion coefficient and low thickness, a distorted curve is obtained. Thus the diffusion apparatus is tested in order to assess its distortion effect on the experimental curve. The testing consists of measuring the apparatus response to a short impulse of the penetrating agent.
The resulting apparatus response, f(t) is usually normalized with respect to the total amount of penetrating agent; the true form of the experimental curve can be obtained by solving the first-order Fredholm equation
 |
(1) |
where f(t) is the experimentally registered curve,
Y(t) is the true curve, and f(t) is the response of the apparatus to the short-time pulse. Curves 1-3 in Fig. 6, correspond to the
f(t), f(t) and Y(t) curves, respectively, for a gas permeability experiment. The presence of statistical errors in the experiment makes it impossibile to find the exact solution of eqn. (1), or to determine the incorrectness of the task. The solution of eqn. (1) has been found by means of the method of one-parameter regularization, but only to within the accuracy of the experimental measurements.
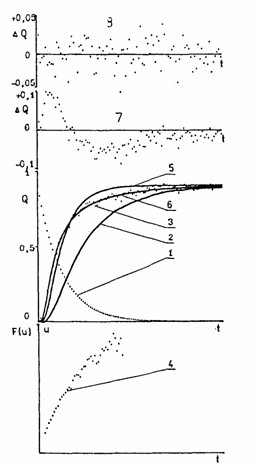 Fig. 6. Evaluation of the gas permeability measurements on polymer membranes. Curves: (1) response of the apparatus to a gas impulse; (2) experimental curve representing the time dependence of the inertia of the apparatus; (3) experimental curve; (4) experimental curve plotted on the functional scale; (5) computed curve based on the classical diffusion mechanism (inadequate in this case); (6) computed curve based on the parallel diffusion mechanism (adequate in this case); (7) drift of residues from the baseline corresponding to curve 5; (8) drift of residues from the baseline corresponding to curve 6.
Fig. 6. Evaluation of the gas permeability measurements on polymer membranes. Curves: (1) response of the apparatus to a gas impulse; (2) experimental curve representing the time dependence of the inertia of the apparatus; (3) experimental curve; (4) experimental curve plotted on the functional scale; (5) computed curve based on the classical diffusion mechanism (inadequate in this case); (6) computed curve based on the parallel diffusion mechanism (adequate in this case); (7) drift of residues from the baseline corresponding to curve 5; (8) drift of residues from the baseline corresponding to curve 6.
It can be seen from curves 2 and 3 in Fig. 6 that the inertia of the apparatus causes an important distortion of the experimental curve, a time delay and a decrease in the flux Q(f) of the penetrating agent through the membrane. Unfortunately, when the systematic errors of the experiment are taken into account, the statistical errors of the experiment increase. Consequently, it is necessary to use a dynamic and precise apparatus for diffusion measurements on membrane materials.
Evaluation of experimental results on the basis of the classical diffusion model
After reconstructing the true experimental curves the diffusion parameters can be evaluated. Several methods for doing this are discussed here.
The method of linearization [7] is based on the application of functional scales. For the results of gas-permeability measurements the following expression can be used to construct the functional scale
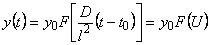 |
(2) |
where t0 is the time of the onset of diffusion (U=
Dt/l2) and the function F(U) is given by
 |
(3) |
By means of eqn. (3) the function F(U) can be evaluated; equal intervals of the function
F(U) are established and the corresponding values of U are found. The values of
U and F(U) are plotted on the ordinate axis, the former on the right, the latter on the left; time t is plotted on the abscissa.
Using the functional scale constructed in this way, the experimental values are normalized with respect to the steady-state gas flux; i.e.
F(U) = l(t)/Q�. Curve 4 in Fig. 6 is an example of a linearized curve obtained from gas permeation experiments; curve 3 in Fig. 6 represents the true experimental curve on the normal scale. The linear dependence shown in Fig. 6, curve 4 is described by the function
U= (D/l2) �(t � t0); the diffusion coefficient
D can be evaluated from D = l2(tg
a) where tg a is the slope of the linearized dependence.
From curve 4 in Fig. 6 it follows that the gas diffusion across the membrane is characterized by two different values of the diffusion coefficient which correspond to the model of the diffusion through two independent channels.
Typical experimental curves obtained by means of various gas permeability methods are shown in Fig. 1: namely (a) the integral method, (b) the differential method, (c) the impulse method, and (d) the differential impulse method. Using the experimental data obtained with these methods, a preliminary assessment of the diffusion parameters can be made by using the "method of particular points".
With the integral method, the point q (see Fig. l(a)), determined by extrapolating the linear part of the curve to its intersection with the abscissa, can be used. With the differential method the point
t1/2 (see Fig. l(b)), which corresponds to half the concentration of the gas at the membrane input, can be used. When the impulse and differential impulse methods are used, the points tm and ti, can be determined from the corresponding experimental curves (see Fig. l(c) and l(d)). Any of these points can be used to determine the diffusion coefficient
D, using
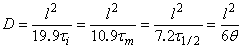 |
(4) |
supposing that
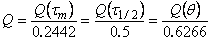 |
(5) |
where l is the thickness of the membrane.
The homogeneity of the diffusion medium can simply be assessed by using these "particular points". For a homogeneous polymer membrane all values of the diffusion coefficient calculated from eqn. (4) are identical. For non-homogeneous membranes where some diffusion paths lead to enhanced diffusion and to short diffusion times, the values of
D calculated from eqn. (4) differ.
A rapid determination of the diffusion coefficient can be made (even before the steady state is attained) by using the particular point
tm:
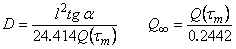 |
(6) |
where tg a is the slope of the linear part of the curve extrapolated to the point
tm.
The "method of statistical parameters" is based on the supposition that any function depending, on time (and tending to a constant value at
t��) can be considered as the integral distribution function of an accidental parameter. This statistical approach enabled us to understand the physical meaning of the "particular points".
Any limited normalized function y=f(t) (y�0,
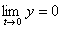 ) may be considered as the density of the accidental parameter; in the case of the impulse method of gas-permeability measurement the density of the distribution is described by
) may be considered as the density of the accidental parameter; in the case of the impulse method of gas-permeability measurement the density of the distribution is described by
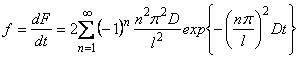 |
(7) |
The integral function F(t), representing the normalized gas flux, is used to determine the statistical parameters
mk according to
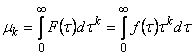 |
(8) |
The universal way of determining the statistical parameters consists in integrating the experimental curves, plotted as
Q vs. t, t2, t3, etc. It should be pointed out that the experimental results must be presented as a set of numerical data (i.e. not as a graphical plot).
The following expressions are valid for the statistical feed parameters of the impulse gas permeability curves:
m1=(l2/6) D = 0, this parameter is called the mean value of the curve;
m2 = (7/5)q2;
m3 = (93/35)q3; and
m4=(1143/175)q4.
The central statistical parameters of the curves are defined as:
M2=(2/5)q2, curve dispersity;
M3 = (16/35) q3, curve asymmetry; and
M4 = (228/175) q4, curve excess.
By means of the statistical parameters a full description of the impulse gas permeability curve can be made. A more generalized description of the curve is possible by using the basic statistical parameters
b1, and b2 which represent the central statistical parameters of asymmetry
M3 and excess M4 normalized with respect to the parameters
M2 (dispersity), i.e.
b1 = M32/M23 = 160/49 = 3.27
b2=M4/M22 =57/7=8.14
Using the coordinates b1 and
b2 all curves of the gas permeability measurements can be transformed into one point only, determined by the coordinates
b1 = 3.27 and
b2 = 8.14. The "diffusion map" is demonstrated in Fig. 7, the point discussed above being designated by the number 6.
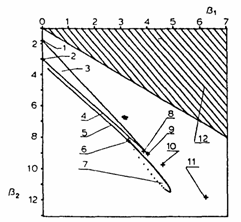 Fig. 7. Diffusion map representing various cases of the gas permeability of polymer membranes. Curves: (1) uniform distribution; (2) normal distribution; (3) region of fl distribution; (4) -c distribution; (5) permeability model plus an irreversible first-order chemical reaction between the gas and the membrane traps (permanent trapping); (6) permeability model; (7) permeability model based on parallel diffusion; (8) permeability measured by means of the electrochemical method; (9) exponential distribution (single-jump diffusion, kinetic stage of diffusion).
Fig. 7. Diffusion map representing various cases of the gas permeability of polymer membranes. Curves: (1) uniform distribution; (2) normal distribution; (3) region of fl distribution; (4) -c distribution; (5) permeability model plus an irreversible first-order chemical reaction between the gas and the membrane traps (permanent trapping); (6) permeability model; (7) permeability model based on parallel diffusion; (8) permeability measured by means of the electrochemical method; (9) exponential distribution (single-jump diffusion, kinetic stage of diffusion).
It is obvious that the expressions for the statistical parameters are much simpler than the initial expressions describing the kinetics of diffusion. Hence, the application of the method of statistical parameters to the evaluation of diffusion and related parameters is rapid and easy.
Choice of a more suitable phenomenological model of gas diffusion
In the case where the experimental data treated so far do not correspond to the classical diffusion model, an alternative more adequate diffusion model must be chosen for the determination of the diffusion coefficient. The basic expressions necessary for the computer treatment are stored in a special "bank of phenomenological diffusion models". The choice of an adequate diffusion model is made by a step-wise trial of various models, starting from a simple one and going on to more complicated models.
The general equation that is used to describe the various diffusion situations and diffusion models is
|
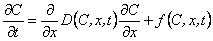
|
(9) |
The analytical and numerical solutions of diffusion equations are stored in the bank of phenomenological models, taking into account both the irreversible and reversible chemical reactions of first and second order between the gas and the traps in the solid, the various cases of parallel diffusion, dissociation, diffusion (including the exchange of diffusing gas between the diffusion channels), etc. In the solutions of the diffusion equations, various concentration profiles of the gas in the membrane, various concentration and time dependences of the diffusion parameters, etc. are considered.
The choice of an adequate phenomenological model of diffusion is made by means of standard methods of mathematical statistics, e.g. using the Fischer criterion (which involves comparing the dispersity parameter
M2 of the curve with the remaining sum of deviations for the corresponding point on the curve). A diffusion model is considered to be adequate when the difference between the experimental curve and the theoretically constructed curve corresponds to a normal distribution, and no drift of residues is observed.
As shown by Fig. 6, the theoretical curve computed using the
classical diffusion model (curve 4, Fig. 6) does not fit well with the
experimental curve (curve 3, Fig. 6) and there are differences between the
experimental and theoretical curves (curve 7, Fig. 6). A systematic drift of
residues from the baseline was observed (curve 7, Fig. 6), indicating that the
classical diffusion mechanism is inadequate in this case.
From the linearized plot (curve 4, Fig. 6) it follows that the model of parallel diffusion is more suitable. The fitness of this diffusion model is proven by the coincidence of the theoretical and experimental curves (curves 6 and 3, respectively, in Fig. 6).
A large number of experimental curves is stored in the bank of experimental data (BED) which we have organized. The necessary condition for this storage is the standardization of the experimental data. In the bank of experimental data both the shape of the experimental curve and the conditions of the measurements are stored. The classical diffusion model is used as the reference for the comparison of curves.
The condensed shape of any experimental curve can be determined using
|
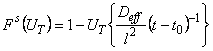
|
(10) |
where the values of U are given.
The determination is based on the analysis of the drift of residues from the baseline and the evaluation of the relative deviation of
D from the average diffusion coefficient, Deff calculated using the experimental data of the whole curve. The service programs for the computer treatment of the experimental data are used.
The advantages of using condensed information in the form of a "diffusion map" should be mentioned here. The diffusion model is determined simply from the position of the point on the plot b1 vs. b2 which represents the whole experimental curve. Using a diffusion map it is possible to forecast changes in the diffusion curve which may be caused by the influence of various effects on the system being investigated. The relationship between various diffusion mechanisms can be established. Moreover, the existence of "white spots" on the diffusion map stimulates the search for mechanisms of gas diffusion in solids which have not yet been discovered. A part of a diffusion map representing several diffusion mechanisms of gas permeability is shown in Fig. 7.
CONCLUSION
A large number of experimental techniques for investigating polymer selective membranes have recently been suggested. Methods based on the diffusion of gases through membranes represent a powerful tool for investigating the dynamic properties of membranes. The existing information obtained from experimental data and the phenomenological models of the diffusion mechanisms are stored in the computer information bank and can be used to evaluate new experimental data. The DIGS computer programs suggested enable preliminary treatment of experimental results, and evaluation of the diffusion characteristics related to the adequate diffusion mechanism.
REFERENCES
- K.B. Zaborenko, L.L. Melichov and V.A. Portyanoy, Radiokhimia, 7 (1965) 319.
- K.B. Zaborenko and I.N. Beckman, Radiokhimia, 10 (1968) 268, 382.
- V. Baiek and J. Tolgyessy, Emanation Thermal Analysis and Other Radiometric Methods, in Wilson and Wilson (Eds.), Comprehensive Analytical Chemistry, Vol. XI1C, Elsevier, Amsterdam, 1984, 302 pp.
- I.N. Beckman and V. Baiek, Symposium on Separation Polymer Membranes, Tokyo, 1987.
- I.N. Beckman, I.P. Romanovski and V. Baiek, Proc. 29th Microsymposium on Synthetic Polymer Membranes, Prague, 1986, p. 24.
- I.N. Beckman, A.A. Shviryaev and V. Balek, in: Proc. 29, Microsymposium on Synthetic Polymer Membranes, Prague 1986, p. 36.
- I.N. Beckman, A.A. Shviryaev and V. Balek, Thermochim. Acta, 104 (1986) 255.
- I.N. Beckman, in Diffusion Phenomena in Polymers, Publ. House of USSR Academy of Sciences, 1985, p. 44.
 Fig. 1. Typical experimental curves resulting from various gas permeation methods. Curves 1 and 2 correspond to the time dependences of the partial pressure of the diffusion agent on the membrane input and that of the gas flux through the membrane, respectively, (a) Integral method: (b) differential method; (c) impulse method; (d) differential impulse method.
Fig. 1. Typical experimental curves resulting from various gas permeation methods. Curves 1 and 2 correspond to the time dependences of the partial pressure of the diffusion agent on the membrane input and that of the gas flux through the membrane, respectively, (a) Integral method: (b) differential method; (c) impulse method; (d) differential impulse method.


 Fig. 5. Experimental results of the inert gas probe method using a set of rectangular pulses of
222Rn. Curves: (1) value of the inert gas concentration at the membrane input; (2 and 3) changes in the inert-gas flux at the membrane output in the case of a stable and unstable membrane, respectively.
Fig. 5. Experimental results of the inert gas probe method using a set of rectangular pulses of
222Rn. Curves: (1) value of the inert gas concentration at the membrane input; (2 and 3) changes in the inert-gas flux at the membrane output in the case of a stable and unstable membrane, respectively.
 Fig. 6. Evaluation of the gas permeability measurements on polymer membranes. Curves: (1) response of the apparatus to a gas impulse; (2) experimental curve representing the time dependence of the inertia of the apparatus; (3) experimental curve; (4) experimental curve plotted on the functional scale; (5) computed curve based on the classical diffusion mechanism (inadequate in this case); (6) computed curve based on the parallel diffusion mechanism (adequate in this case); (7) drift of residues from the baseline corresponding to curve 5; (8) drift of residues from the baseline corresponding to curve 6.
Fig. 6. Evaluation of the gas permeability measurements on polymer membranes. Curves: (1) response of the apparatus to a gas impulse; (2) experimental curve representing the time dependence of the inertia of the apparatus; (3) experimental curve; (4) experimental curve plotted on the functional scale; (5) computed curve based on the classical diffusion mechanism (inadequate in this case); (6) computed curve based on the parallel diffusion mechanism (adequate in this case); (7) drift of residues from the baseline corresponding to curve 5; (8) drift of residues from the baseline corresponding to curve 6.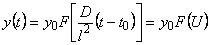

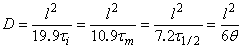
 Fig. 7. Diffusion map representing various cases of the gas permeability of polymer membranes. Curves: (1) uniform distribution; (2) normal distribution; (3) region of fl distribution; (4) -c distribution; (5) permeability model plus an irreversible first-order chemical reaction between the gas and the membrane traps (permanent trapping); (6) permeability model; (7) permeability model based on parallel diffusion; (8) permeability measured by means of the electrochemical method; (9) exponential distribution (single-jump diffusion, kinetic stage of diffusion).
Fig. 7. Diffusion map representing various cases of the gas permeability of polymer membranes. Curves: (1) uniform distribution; (2) normal distribution; (3) region of fl distribution; (4) -c distribution; (5) permeability model plus an irreversible first-order chemical reaction between the gas and the membrane traps (permanent trapping); (6) permeability model; (7) permeability model based on parallel diffusion; (8) permeability measured by means of the electrochemical method; (9) exponential distribution (single-jump diffusion, kinetic stage of diffusion).