Радиохимия, т.24, №1 (1982) 126-134
УДК 546.296: 539.217.5: 678.742.3: 778.33
И. Н. БЕКМАН, А. А. ШВЫРЯЕВ
Авторадиографический вариант метода проницаемости, основанный на одновременном использовании радиохимической модификации метода газопроницаемости и метода авторадиографии, использован для анализа сложных диффузионных процессов в твердых телах. Изучены топологические особенности диффузии радона в полипропилене крупносферолитной структуры. Обнаружено существование сильной, как пространственной, так и временной, неоднородности диффузионного процесса. Для двух времен диффузии рассчитаны спектры безразмерных времен диффузии. Установлено, что все спектры имеют сложную непрерывную структуру, связанную с наличием в образце набора диффузионных путей, характеризующихся различными значениями сорбционной способности и фактора извилистости. Обсуждены некоторые методические трудности, возникающие при использовании авторадиографического варианта метода проницаемости для анализа процессов диффузии в сложных средах.
Хорошо известно, что метод газопроницаемости весьма чувствителен к наличию в мембране макродефектов. Например, при изучении влияния морфологической структуры полимера на скорость диффузии различных газов в полипропилене [1] было обнаружено резкое возрастание проницаемости пленок при диаметрах сферолитов свыше 100 мкм. Детальный анализ полученных результатов показал, что релаксация напряжений в процессе приготовления мембраны приводит к появлению на границах сферолитов микропустот и трещин. Вначале они внутренние, но постепенно становятся сквозными, вызывая увеличение потока газа через мембрану. Наличие нескольких диффузионных путей в образце приводит к искажению формы кинетических кривых и затрудняет расчет диффузионных параметров. Поэтому представляет интерес разработка способов выявления такого рода аномалий и создание алгоритмов их качественной интерпретации.
Настоящая работа посвящена совместному использованию радиохимического варианта метода проницаемости и метода авторадиографии (АРГ) для анализа сложных диффузионных процессов в твердых телах. Методику отрабатывали на примере диффузии радона в полипропилене крупносферолитной структуры.
Все эксперименты проводили на одной мембране из изотактического полипропилена. Образец готовили путем горячего прессования. С этой целью полимер 30 мин выдерживали при 250 °С и давлении 5•10-6 Па с последующей термической кристаллизацией при 145 °С в течение 8 ч. Путем фотографирования мембраны в поляризованном свете установлено, что структура пленки представлена отдельными крупными сферолитами, достигающими в диаметре 400 мкм, распределенными среди сферолитов размером 20-30 мкм.
Диффузионные характеристики определяли изостатическим вариантом метода проницаемости. В процессе эксперимента регистрировали зависимость от времени потока радона через мембрану. При этом было обнаружено аномальное поведение кривых «прорыва». 1. Диффузионный процесс достигает стационарного состояния значительно быстрее, чем можно было бы ожидать из результатов предварительной работы по изучению проницаемости радона через полипропилен с различной термической предысторией. 2. Кривые неудовлетворительно спрямляются в линеаризованном масштабе. 3. Коэффициенты диффузии, рассчитанные по «особым» точкам, не совпадают друг с другом. Например, Dtпрор = 1.5×10-7 см2/с, Dtпер = 1.2 ×10-7 см2/с, Dt1/2 = 1.0×10-7 см2/с, Dq = 8.9 ×10-8 см2/с, т. е по мере приближения к стационарному состоянию потока коэффициент диффузии систематически уменьшается. Отметим, что даже самое низкое значение коэффициента диффузии все же значительно превышает соответствующую величину для мелкосферолитного полипропилена (D=0.9×10-8 см2/с).
Полученные данные свидетельствуют о наличии нескольких диффузионных путей в мембране. Однако попытки использования нелинейного метода наименьших квадратов для разложения сложной кинетической кривой на отдельные компоненты не увенчались успехом. По-видимому, спектр коэффициентов диффузии имеет сложную непрерывную структуру, для разрешения которой следует использовать специальные методы.
Для решения поставленной задачи мы воспользовались авторадиографическим вариантом метода проницаемости. При проведении эксперимента по этому методу диффузионный процесс прерывали в некоторый момент времени, мембрану вынимали и зажимали между двумя фотопластинками. После экспонирования и проявления пластинки фотометрировали. Данные получали при двух временах диффузии: t1=160 с, которое примерно соответствовало t1/2, т. е. времени достижения потоком значения Qt = 0.5Q¥, и t2 = 220 с, т. е. несколько выше времени запаздывания q (поток Qt = 0.7Q¥). В работе использовали фотоэмульсию, чувствительную только к a-излучению. Ширина щели фотометра составляла 10 мкм. Поскольку пробег a-частиц в полипропилене Ra @ 35 мкм, а толщина мембраны составляла H=100 мкм, то распределение примеси на участке в центре мембраны недоступно для регистрации на фотопластинках. Поэтому авторадиограммы содержат информацию только о части пространственного распределения примеси. Тем не менее, данные АРГ позволяют получить сведения об основных топологических особенностях диффузионного процесса.
Уже визуальное рассмотрение авторадиограмм под микроскопом демонстрирует неоднородный характер распределения a-треков как на входе, так и выходе из образца. Основной особенностью является образование скоплений треков, в том числе и упорядоченных типа «звезд». Для выяснения причин появления неоднородностей почернения проводили совмещение АРГ и фотографий того же участка полимерной пленки в поляризованном свете. Прежде всего оказалось, что неоднородности почернения охватывают площади, значительно превышающие размеры сферолитов. Появление таких больших отклонений, возможно, связано с наличием температурного градиента по поверхности мембраны, возникающего в процессе прессования, которое в свою очередь приводит к возникновению областей с различной плотностью, а следовательно, и с различной степенью кристалличности. Определенную роль, возможно, играют и флуктуации в толщине мембраны. Скопления типа «звезд» возникают, как правило, на входной стороне мембраны и главным образом на границах сферолитов. Существование таких скоплений показывает, что в полимере имеются места чрезвычайно активные к сорбции газа. Таких мест может быть достаточно много, так что «звезды» в свою очередь образуют скопления. Скопления звезд располагаются на границах сферолитов. Возможно, что такие звезды представляют собой включения радона в микропузырьки, присутствующие в полимере. Скопления радона не проходят через пленку, так что на стороне, из которой выходит газ, они практически не встречаются, а если встречаются, то не имеют характерного зачерненного центра.
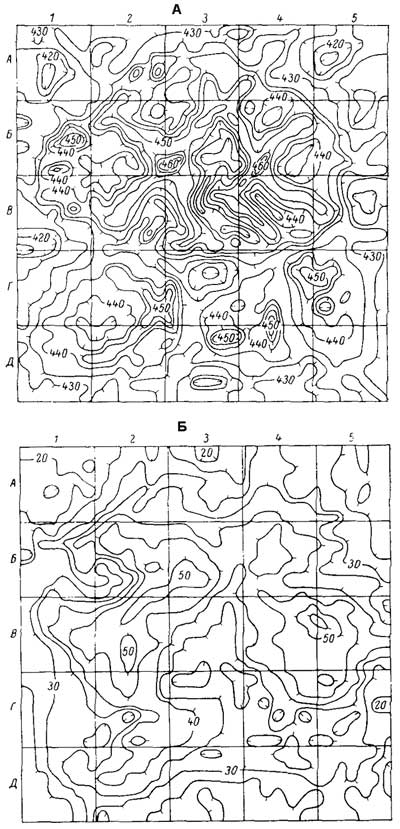
Совокупность кривых фотометрирования позволяет построить топологические карты почернения. С этой целью на АРГ выбирали участок размером 600х600 мкм, расположенный примерно в середине мембраны, разбивали его на 900 одинаковых квадратов и определяли среднее значение плотности почернения в каждом квадрате. Всего таким образом были получены четыре матрицы значений (при двух временах диффузии), которые в дальнейшем использовали для расчета диффузионных параметров. Полученные результаты представлены на рис. 1 в виде изолиний, проведенных через одинаковые значения плотности почернения. Как следует из рис. 1, вся площадь мембраны охвачена процессами сорбции и диффузии. Распределение плотности почернения имеет неравномерный характер: присутствуют как крупные региональные, так и многочисленные локальные аномалии. Насколько можно судить, региональные аномалии отражают топологические особенности структуры мембраны. Неровности рельефа выражены в максимальной степени на входной стороне мембраны при t1, а в минимальной - на выходной стороне мембраны при времени t2.


Рис. 1. Результаты фотометрирования авторадиограммы (радон в полипропилене крупносферолитной структуры).
А — входная сторона мембраны, время t1
= 160 c; Б — выходная сторона мембраны, время t1
= 160 c; В — входная сторона мембраны, время
t1 = 220 с; Г — выходная сторона мембраны, время
t1 = 220 с.
Основные черты региональных возмущений на всех АРГ сохраняются, однако в процессе диффузии они сглаживаются, подтверждая наличие сильной боковой диффузии. Возможно, что при стационарном состоянии будет достигнуто практически равномерное распределение концентрации на выходной поверхности мембраны.
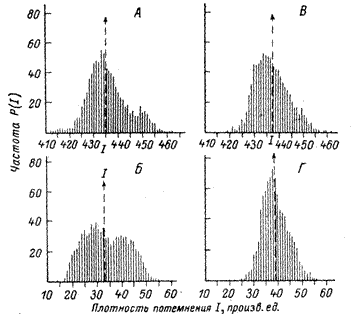 Рис. 2. Выборка из результатов фотометрирования авторадиограммы.
А — входная сторона мембраны, время t1=160 c; Б — выходная сторона мембраны, время
t1=160 c; В — входная сторона мембраны, время t1=220
с; Г — выходная сторона мембраны, время t1=220 с.
Рис. 2. Выборка из результатов фотометрирования авторадиограммы.
А — входная сторона мембраны, время t1=160 c; Б — выходная сторона мембраны, время
t1=160 c; В — входная сторона мембраны, время t1=220
с; Г — выходная сторона мембраны, время t1=220 с.
Определенную информацию о топологических особенностях диффузии можно получить из плотности распределения степени почернения. Соответствующие распределения частот для выборок из результатов сканирования приведены на рис. 2. Рассчитанные по стандартной методике [2] начальные, центральные и основные статистические моменты плотности распределения собраны в таблице. Полученные результаты позволяют сравнить распределения сводных результатов сканирования с такими хорошо известными распределениями, как гауссовское (для которого нормированная асимметрия b1=(m32/m23)=0, нормированный эксцесс b2=(m4/m23)=3, где m3 — третий центральный момент или асимметрия распределения; m4 — четвертый центральный момент или крутизна в моде; m2 — дисперсия) и равномерное (b1=0, b2=l.8) распределения. Как следует из таблицы, функция распределения для всех плотностей почернения носит асимметричный характер, особенно на входной стороне мембраны. В ходе диффузии распределение I на выходной поверхности мембраны переходит от формы, характерной для равномерного распределения, к форме, более близкой к гауссовской (хотя правосторонняя асимметрия все же сохраняется, и пики более плоские, чем должны быть в чисто нормальном распределении). Во всех случаях заметно присутствие аномально больших значений плотности почернения.
|
Условия эксперимента |
Математическое ожидание |
Дисперсия |
Основные моменты |
|
|
m'0 |
m2 |
b1 |
b2 |
|
|
|
Плотность потемнения |
|||
| Время диффузии t1=160c Вход мембраны Выход мембраны |
4.49×102 3.68×102 |
6.95×101 7.43×101 |
0.194 0.016 |
2.97 2.06 |
| Время диффузии t2=220 с Вход мембраны Выход мембраны |
4.49×102 2.79×102 |
5.02×101 2.83×101 |
0.153 0.107 |
2.84 2.74 |
|
Безразмерное время диффузии |
||||
| Время диффузии t1=160c | 2.04 | 1.62 ×10-3 | 0.65 | 3.11 |
| Время диффузии t2=220с | 1.96 | 9.14 ×10-4 | 1.63 | 5.31 |
Данные по почернению на входной и выходной поверхностях мембраны позволяют рассчитать спектр безразмерных времен диффузии: u=Dt/P (1), где D - коэффициент диффузии, t - время диффузии, I - длина диффузионной трубки тока (в первом приближении можно принять, что 1=Н, где Н - толщина мембраны).
При определении спектра u для каждого i-го участка мембраны рассчитывали нормированную плотность почернения:
|
|
(2) |
где Iвых(уi,zi) и Iвх(уi,zi) — значения почернений на взаимопротивоположных точках мембраны. Далее решали относительно С(х, u) интегральное уравнение
 |
(3) |
где С (х, и) — распределение концентрации радона по толщине мембраны:
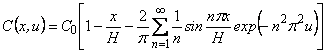 |
(4) |
К(x, Н-х) — ядро уравнения Фредгольма 1-го рода (аппаратурная функция).
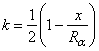 |
(5) |
Ra@35 мкм - пробег a-частиц радона в полипропилене. Из C(x,u) вычисляли непосредственно параметр и.
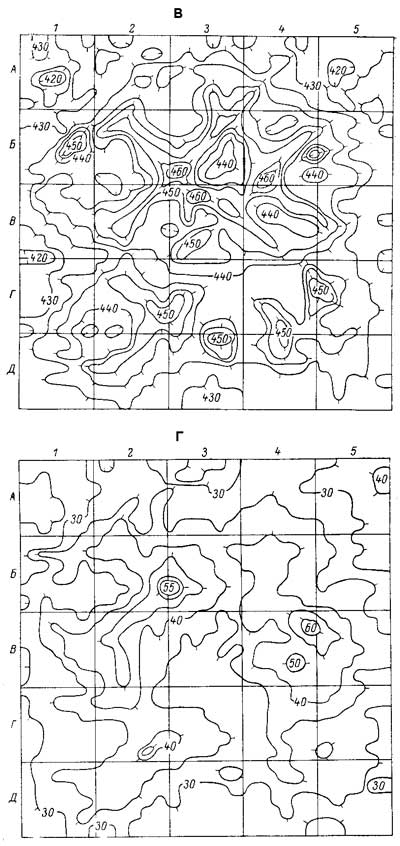
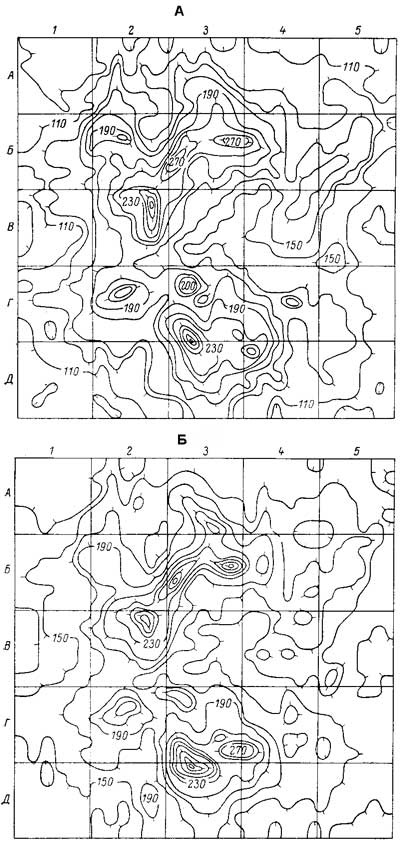 Рис.3 Распределение безразмерных времен диффузии по поверхности мембраны.
Рис.3 Распределение безразмерных времен диффузии по поверхности мембраны.
А – время диффузии t1=160 c; Б – время диффузии t2=220 c
Топологические диффузионные карты приведены на рис. 3. Видно, что распределение и по поверхности мембраны носит сильно неравномерный характер, особенно при малых временах диффузии. Основные особенности рельефа аналогичны для всех времен диффузии, хотя в ходе процесса амплитуды возмущений уменьшаются, а локальные аномалии исчезают. Сравнение с картами плотностей почернения (рис. 1) обнаруживает существенные различия в характере рельефа. Лишь одна область (квадраты Б2, ВЗ, В2) четко проявляются на обоих рисунках. Заметная на рис. 1 аномалия в квадрате B4 практически отсутствует на рис. 3, а аномалия в квадрате Г2 значительно ослаблена. Обращает на себя внимание сильное возмущение в квадратах ГЗ, ДЗ и Д4 на карте распределения и, где достигается максимальная высота рельефа. Этого возмущения на авторадиограммах не было.
Сводные результаты по выборкам параметра и приведены на рис. 4, а значения статистических моментов - в таблице. Видно, что спектры имеют непрерывный характер и обладают правосторонней асимметрией (особенно при больших временах диффузии), причем ни один из спектров не удается описать гауссовским или равномерным распределением. Отметим, что спектр Р (и) более подвержен статистическим флуктуациям, чем спектр I.
Интересно провести сравнение данных для авторадиографического варианта метода проницаемости с данными, полученными из кинетических кривых прорыва. Как следует из рис. 4, расчеты по ранним временам (например, по tпрор) дают оценку верхней границы спектра, связанную, вероятно, с диффузией по макродефектам. Вычисления и по большим временам диффузии лучше отражают характер спектра, поскольку в рассмотрение вовлекаются низкие коэффициенты диффузии. Ближе всего как к математическому ожиданию, так и к моде распределения оказывается значение и, определенное по t1/2. Это еще раз подтверждает известный принцип, что расчеты следует проводить по медиане распределения (как известно, t1/2 - медиана распределения, описывающего кривую прорыва). Отметим, что даже последняя «особая» точка - время запаздывания q (математическое ожидание кривой прорыва) - не дает надежной оценки нижней границы спектра.
Основным преимуществом авторадиографического варианта метода проницаемости является возможность раздельного определения спектра констант растворимости Р(Кр) и спектра коэффициентов диффузии Р(D). Действительно, распределение плотности почернения на входе мембраны Р(Iвх) при малых временах (а при малых Ra - практически при всех временах) отражает спектр Р(Кр). В ходе диффузии на спектр Р(Кр) накладывается спектр Р(D). Спектр на выходе мембраны Р(Iвых) связан со спектром Р(Kр-D). Рассчитав спектр нормированных плотностей почернения Р(F), найдем спектр Р (D). К сожалению, применение этой простой схемы Iвых/Iвх®С®и®D сталкивается со значительными трудностями при исследовании таких сложных сред, как полипропилен крупносферолитной структуры. Рассмотрим некоторые особенности авторадиографического варианта метода проницаемости, затрудняющие интерпретацию экспериментальных результатов.
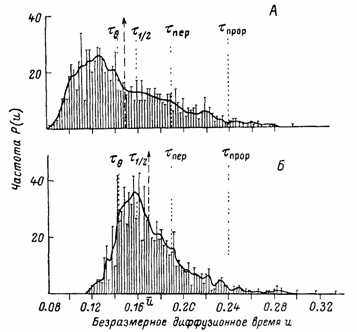 Рис. 4. Функция распределения частот для безразмерного времени диффузии.
Рис. 4. Функция распределения частот для безразмерного времени диффузии.
А — время диффузии t1=160 c; Б — время диффузии t2=220 c
Первый этап: переход F ® и. На этом этапе важен оптимальный выбор времен диффузии, первичная обработка двумерной информации и разграничение поступательной и боковой диффузии. 1. Хорошо известно, что в методе АРГ изображение размывается за счет конечной величины пробега. В результате спектр Р (F) оказывается неадекватным истинному распределению концентрации. Для восстановления действительного вида распределения следует проводить редукцию на аппаратурную функцию, используя для этой цели двумерное уравнение Фредгольма. В нашем случае пробег Ra =35 мкм, изображение дискретизировалось квадратами 20х20 мкм, и влияние точечного источника распространялось только на два квадрата, в связи с чем данным видом искажения можно было пренебречь. Однако при работе с более жесткими излучателями ошибки за счет этого фактора могут стать значительными. 2. Обнаруженная в настоящей работе сильная боковая диффузия приводит к искажению спектра Р(и): причем отношение F=Iвых/Iвх может как уменьшаться, так и увеличиваться в зависимости от того, в какой области профиля мембраны происходит отклонение диффузионного потока от прямолинейного пути. Из-за этого эффекта возможно появление значений F, превышающих предельную величину F для стационарного состояния, а следовательно, и значений u=¥. Особенно сильное влияние могут оказывать микропустоты, аккумулирующие радиоактивный газ. Появление пустот вблизи входной поверхности приведет к резкому уменьшению F, а вблизи выходной поверхности - к его увеличению (в последнем случае может быть сделан ошибочный вывод о достижении на данном участке стационарного состояния). 3. При изучении диффузии в сложных средах важнейшее значение имеет правильный выбор времен диффузии. В данной работе результаты получены только для двух времен, что не позволяет достаточно надежно описать развитие диффузионного процесса во времени. Действительно, наименьшее время Диффузии следует выбирать таким образом, чтобы примесь прошла на расстояние, достаточное для ее надежной регистрации со стороны выходной поверхности мембраны. С этой точки зрения выбор времени t1 был правильным - вся поверхность мембраны охвачена диффузией. Однако в связи с тем, что спектр Р(и) оказался очень широким, часть значений и попала в неустойчивую область вблизи стационарного состояния. В этой области флуктуации и значительно превышают флуктуации F(и), и верхняя граница спектра Р(и) отягощена большими ошибками.
Второй этап: переход и®D. На первый взгляд проблема эта решается просто: если принять условие 1=Н, то в выражении (1) неизвестно только D. При таком формальном подходе получены следующие характеристики спектра локальных коэффициентов диффузии: для времени t1 – Dмин=5.2×10-8 см2/с; D=9.4×10-8 см2/с; Dмакс=1.9×10-7 см2/с, а для времени t2 – Dмин=5.3×10-8 см2/с; D=7.8 ×10-8 см2/с; Dмакс=1.5×10-7 см2/с, или после усреднения: Dмин=5.2×10-8 см2/с; D=8.6 ×10-8 см2/с; Dмакс=1.7×10-7 см2/с. Сравнение с результатами, полученными из кривой прорыва, Dtпрор=1.5 ×10-7 см2/с;D0==9.0 ×10-8 см2/с, показывает, что из кинетических данных можно получить правильную оценку верхней границы спектра и среднее значение коэффициентов диффузии, однако нижняя граница спектра практически не влияет на форму кривой прорыва. Поэтому выявить наличие низких коэффициентов диффузии можно только с помощью авторадиографического варианта метода проницаемости.
При работе со сложными средами переход и®D представляет собой некорректно поставленную задачу, при решении которой возникают серьезные трудности. 1. Даже в случае выполнения условия 1=Н для расчета локальных коэффициентов диффузии необходимо знать значения локальных толщин мембраны. Провести подобные измерения Н практически невозможно (в нашем случае на участке площадью З.6×10-3 см2 необходимо определить 900 значений Hi). Поэтому даже при известном значении средней толщины мембраны H, рассчитанной из данных для различных достаточно удаленных друг от друга точек мембраны, ее ошибки (в нашем случае d=4%) и функции распределения Р(H) все же остается некоторая некорректность при переходе к Р(D). 2. При диффузии в сложной среде дисперсионного типа условие 1=Н не выполняется в связи с наличием непроницаемых кристаллитов и сферолитов с полупроницаемыми центрами прямолинейный характер трубок тока нарушается и миграционный путь увеличивается. Тогда 1= xH, где x > 1 - фактор извилистости, нам неизвестный. Поэтому переход и® D невозможен. Лишь для некоторой части спектра Р(и) можно определить локальные коэффициенты диффузии. Проведенные нами предварительные расчеты автокорреляционных и взаимокорреляционных функций для плотностей почернения на входной и выходной поверхностях мембраны позволили выделить участки, для которых наблюдается существенная корреляция между 1вх(уi, zi) и 1вых(уi, zi). Для этих участков условие I=Н справедливо и удается оценить локальные коэффициенты диффузии. Данным методом, в частности, было показано, что в квадратах ВЗ и ДЗ (рис. 3) происходит сквозная, ненарушенная сферолитами диффузия. Поскольку именно для этих областей достигаются максимальные значения и, то, по-видимому, они представляют собой сквозные макродефекты, ответственные за возрастание проницаемости полипропилена при увеличении размеров сферолитов. 3. В настоящей работе обнаружено, что не вся примесь, зарегистрированная на входе мембраны, участвует в диффузионном процессе. Действительно, сравнение карт и для двух времен диффузии (рис. 4, а и 4, б) показывает, что значительная часть локальных потоков при времени уже достигла стационарного состояния. Однако этот вывод противоречит значениям F (и) для тех же координат, которые были всегда ниже Fстац. Это противоречие можно объяснить, только предположив, что некоторое количество адсорбированной на входной поверхности мембраны примеси не принимает участия в диффузии. Наблюдаемые эффекты могут быть вызваны участками образца, обладающими аномально высокой сорбционной способностью, газовыми пузырьками или радиоактивными продуктами распада радона.
Таким образом, при современном состоянии методического обеспечения авторадиографического варианта метода проницаемости удается получить количественную информацию о топологических особенностях процесса растворения и диффузии только в тех относительно простых системах, в которых боковая диффузия полностью подавлена и длина трубки тока примерно соответствует толщине мембраны. Для анализа сложных диффузионных процессов необходимо провести дальнейшую разработку теоретических основ метода, например, привлечь методы аналитического продолжения концентрационных полей.
Однако уже результаты настоящей работы показывают, что предложенный метод позволяет получать информацию о процессах переноса, недоступную для традиционных вариантов метода проницаемости. Так, удалось продемонстрировать сложный характер процессов растворения и диффузии, выявить роль сферолитов, оценить вид спектра коэффициентов диффузии и доказать непрерывность его структуры, обнаружить существование на входной поверхности мембраны неподвижных состояний примеси, установить наличие сильной боковой диффузии, по-видимому связанной с огибанием диффузионным потоком плотных центров сферолитов, выявить наличие сквозных каналов, микропузырьков и т. п. Поэтому нам представляется возможным уже на данном этапе рекомендовать авторадиографический вариант метода проницаемости для анализа сложных диффузионных аномалий.