Радиохимия, т.23, №5 (1981) 760-766
УДК 539.217.5: 778.33: 546.286: 7678.742.3
ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИЗУЧЕНИЯ ДИФФУЗИИ РАДИОАКТИВНЫХ ГАЗОВ В ТВЕРДЫХ ТЕЛАХ
V. АВТОРАДИОГРАФИЧЕСКИЙ ВАРИАНТ МЕТОДА ПРОНИЦАЕМОСТИ
И. Н. БЕКМАН
Предложен новый способ определения параметров диффузии радиоактивных газов с твердых телах, основанный на одновременном использовании метода газопроницаемости и метода авторадиографии. Способ предназначен для изучения топологических особенностей диффузионного процесса и определения спектра локальных коэффициентов диффузии. Разработана конструкция установки, предложен соответствующий математический аппарат и испытана методика проведения эксперимента. Авторадиографическим вариантом метода проницаемости определены коэффициенты диффузии радиоактивного инертного газа - радона - в полипропилене. Обнаружено хорошее согласие полученных результатов с данными традиционных методов исследования.
В настоящее время метод авторадиографии (АРГ) применяется как для определения коэффициентов диффузии, так и для получения информации о характере распределения примеси по поверхности или объему образца. К сожалению, использование этого метода в области газовой диффузии наталкивается на значительные трудности, связанные с большой подвижностью газообразующей примеси.
Данная работа посвящена созданию методики одновременного использования радиохимического варианта метода проницаемости и метода авторадиографии для определения параметров диффузии газов в твердых телах. Авторадиографический вариант метода проницаемости отрабатывали на примере диффузии радона (222Rn) в полипропилене.
В качестве объекта исследования использовали изотактический полипропилен с содержанием атактической фракции ниже 1%. Полимер поставлялся в виде гранул, которые перерабатывали в пленки путем прессования в пресс-форме с контролируемым нагревом. С этой целью полипропилен нагревали до 200
°С, прикладывали давление 107 Па и затем образец резко охлаждали. Работу проводили на одной мембране толщиной 110 мкм. Фотографии в поляризованном свете показали, что образец обладает мелкосферолитной структурой со средним диаметром сферолитов 10 мкм.
Эксперименты по авторадиографическому варианту метода проницаемости проводили тремя различными способами.
А. Мембрану помещали в диффузионную ячейку и проводили обычный эксперимент по методу проницаемости. В некоторый момент времени диффузионный процесс прерывали путем резкого охлаждения ячейки до температуры жидкого азота, мембрану вынимали и зажимали между двумя фотопластинками. Экспозицию вели при температуре -50
°С. Предварительно было показано, что в этих условиях миграции примеси не происходит. После экспонирования и проявления фотопластинки фотометрировали. Подобные эксперименты повторяли при различных временах, вплоть до установления стационарного состояния диффузии.
Этот вариант в принципе дает всю информацию, необходимую для полного восстановления пространственного распределения примеси по толщине образца, однако он трудоемок и его применение перспективно только при анализе сложных диффузионных аномалий. Кроме того, при манипуляциях с мембраной возможна некоторая потеря исследуемого газа.
Б. Для предотвращения потери газа в процессе экспозиции, можно воспользоваться диффузионной ячейкой, конструкция которой представлена на рис. 1. В этой ячейке фотопластинка находится в постоянном контакте с мембраной. После заполнения ячейки радиоактивным газом одновременно начинаются процессы диффузии и экспонирования.
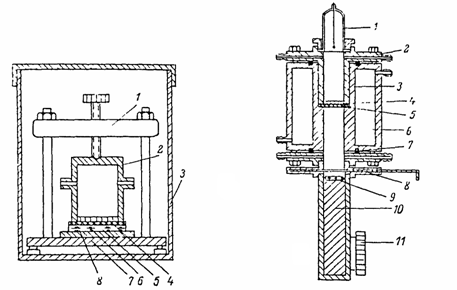 Рис. 1. Устройство для одновременного использования метода газопроницаемости и метода авторадиографии
1 – зажимное устройство; 2 – диффузионная ячейка; 3 – термостатированный корпус; 4 – пористая керамика; 5 – фотопластинка с ядерной эмульсией; 6 – прокладка из губчатой резины; 7 – металлическая пластина; 8 – полимерная мембрана.
Рис. 1. Устройство для одновременного использования метода газопроницаемости и метода авторадиографии
1 – зажимное устройство; 2 – диффузионная ячейка; 3 – термостатированный корпус; 4 – пористая керамика; 5 – фотопластинка с ядерной эмульсией; 6 – прокладка из губчатой резины; 7 – металлическая пластина; 8 – полимерная мембрана.
Рис. 2. Устройство для авторадиографического варианта метода проницаемости.
1 – счетчик радиоактивного излучения; 2 – верхняя секция диффузионной ячейки (резервуар); 3 - нижняя секция диффузионной ячейки (приемник); 4 – подложка из пористой керамики; 5 – мембрана из исследуемого вещества; 6 – термостатируемый объем; 7 – тефлоновое уплотнение; 8 – кассета; 9 – фотопластинка с ядерной эмульсией; 10 – шток вертикального лифта; 11 – система подъема лифта.
Этот вариант применим только в том случае, если излучение из резервуара не доходит или не влияет на материал. Его можно использовать при работе с мягкими
b-излучателями (14С,
3Н и др.) или a-излучателями, причем толщина мембраны должна превышать пробег данного вида излучения в веществе. Для регистрации радона мы использовали эмульсию типа А-2, которая чувствительна к
a-излучению собственно радона, но практически не засвечивается
g- и
b-излучением продуктов его распада. Поскольку процессы диффузии и экспонирования происходят одновременно, то этот метод обладает сильным интегрирующим действием, затрудняющим расчет коэффициента диффузии. Способ прост и его можно рекомендовать для качественного контроля за однородностью диффузионного процесса.
В. Установка, блок-схема которой приведена на рис. 2, позволяет избавиться от большинства указанных выше недостатков. В ней предусмотрена возможность разделения диффузионной ячейки и камеры с фотопластинкой. Ячейка снабжена счетчиком радиоактивного излучения для контроля за активностью на входе мембраны. Со стороны резервуара мембрана поддерживается пластиной из пористой керамики. Тем самым обеспечивается плотный и однородный контакт фотопластинки с мембраной.
В ходе диффузионного процесса приемник продувается сильной струей воздуха (при этом фотопластинка, закрепленная на штоке вертикального лифта, убрана в кассету). В начальный момент времени в резервуар вводили газ и проводили обычный диффузионный эксперимент. Затея кассету открывали, шток поднимали и плотно прижимали фотопластинку к мембране. С этого момента процессы диффузии и экспозиции совпадали. После окончания экспозиции шток опускали, кассету закрывали и удаляли для перезарядки фотоматериала. В данном варианте толщину мембраны выбирали таким образом, чтобы выход на стационарное состояние потока занимал время 1 сут. Удельная активность радона обеспечивала экспозицию 1 час. При этих условиях интегрирующее действие было небольшим и за время эксперимента удавалось получить несколько «кадров» развития диффузионного процесса на определенном участке мембраны.
При использовании тонкой мембраны (Н
= 110 мкм) диффузионный процесс прерывали путем охлаждения ячейки до -40 °С и экспозицию проводили на холоду (при этом резервуар оставался заполненным радиоактивным газом, что предотвращало его потерю из мембраны). Затем фотопластинку удаляли, температуру поднимали до исходного значения и диффузионный эксперимент продолжали.
В варианте В, как и в предыдущем, можно использовать только изотопы с мягким излучением. Его преимущество - в динамичности. При оптимальном выборе толщины мембраны и удельной активности газа возможно снятие полного «фильма» о развитии диффузионного процесса в твердой фазе.
Коротко остановимся на феноменологической теории авторадиографического варианта метода проницаемости. Если выделить в пластинке слои
dr, то излучение dI этого участка в какую-либо сторону
|
dI=C(x, t)AK(x, H-x)dx, |
(1) |
где С (х,t)-распределение концентрации примеси по толщине мембраны;
А - величина, пропорциональная числу частиц, излучаемых данным объемом слоя радиоактивного вещества в единицу времени;
К(х, Н-х) - функция, учитывающая поглощение и отражение излучения материалом мембраны. Плотность почернения фотопластинки на входной стороне мембраны
|
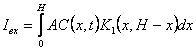 |
(2a) |
а на выходной стороне мембраны
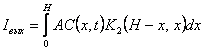 |
(2б) |
Отметим, что при использовании a- или
b-излучения и при H>R
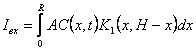 |
(3а) |
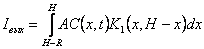 |
(3б) |
Как известно, при традиционных краевых условиях метода проницаемости распределение концентрации диффундирующей примеси по толщине мембраны описывается формулой
|
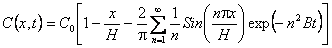 |
(4) |
где С0 - концентрация на входной стороне мембраны, х - координата;
H-толщина мембраны;
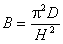 ;
D-коэффициент диффузии.
;
D-коэффициент диффузии.
Для расчета коэффициента диффузии прежде всего следует перейти от измеренной плотности почернения к концентрационному профилю
С (х,t). С математической точки зрения, уравнения (2) или (3) представляют собой интегральные уравнения Фредгольма 1-го. Измерив
Iвх (или Iвых) и зная K1 (или
K2), найдем С(х,t). Поскольку такие задачи относятся к классу обратных, некорректно поставленных задач математической физики, то их решение возможно только при использовании методов регуляризации. С физической точки зрения, ядро уравнения (3),
К (х, Н-х), отражает дозу, создаваемую на фотопластинке излучением от бесконечно тонкого неограниченного слоя активного вещества, расположенного на глубине
х и ориентированного параллельно поверхности мембраны. Для разных видов излучения
К(х,Н-х) описывается различными выражениями. В частности, для
b- и мягкого
g-излучения [1], когда излучение ослабляется как по 1/r2, так и по
е-mr законам,
|
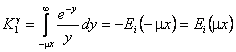 |
(5а) |
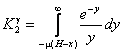 |
(5б) |
где Еi - интегрально-показательная функция;
m - коэффициент ослабления излучения в веществе. Для
a-излучения [2]
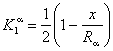 |
(6а) |
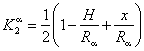 |
(6б) |
где Ra — пробег
a-излучения в веществе; х
£ Ra.
Для демонстрации особенностей метода нами рассчитаны зависимости
Iвх и Iвых от времени диффузии. Вычисления проводили для
14С (Е=0.158 МэВ, m=350-1; Rмакс=300 мкм). Толщина слоя прокладки между мембраной и фотопластинкой
D=10 мкм, толщина мембраны Н=100 мкм, параметр В=1. Как следует из рис. 3, зависимости
Iвх(m) и Iвых(m) имеют параболическую форму и достигают постоянного значения при стационарном состоянии диффузии. Зависимость
F= Iвых/Iвх имеет s-образную форму. На практике использование только
Iвх (или Iвых) встречает серьезные затруднения, поскольку возникает необходимость определения абсолютной удельной активности используемого газа и требуется калибровка функции почернения в единицах активности.
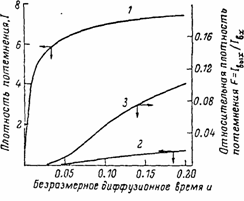 Рис. 3. Зависимость плотностей почернения фотопластинки от безразмерного диффузионного времени.
1 — плотность почернения на входной стороне мембраны; 2 — плотность почернения на выходной стороне мембране; 3 — отношение плотности почернения на выходной стороне мембраны к плотности почернения на входной стороне мембраны. (14С,
Еb=0.158 МэВ,
m=350 см-1, Rмакс = 300 мкм, толщина слоя прокладки между мембраной и фотопластинкой
D=10 мкм).
Рис. 3. Зависимость плотностей почернения фотопластинки от безразмерного диффузионного времени.
1 — плотность почернения на входной стороне мембраны; 2 — плотность почернения на выходной стороне мембране; 3 — отношение плотности почернения на выходной стороне мембраны к плотности почернения на входной стороне мембраны. (14С,
Еb=0.158 МэВ,
m=350 см-1, Rмакс = 300 мкм, толщина слоя прокладки между мембраной и фотопластинкой
D=10 мкм).
Распределение плотности почернения на входной поверхности мембраны может быть использовано для расчета спектров коэффициентов диффузии (точнее для расчета значений безразмерного диффузионного времени, т. е. параметра u=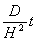 ). Действительно, разброс значений
Iвых, в известном смысле отражает развитие диффузионного процесса на конкретном участке мембраны. Однако такой подход возможен, только если неоднородность почернения связана исключительно с, неоднородностью диффузионного процесса. В случае наличия спектра констант растворимости
Кр плотность почернения Iвых
~ КрD, и для расчета спектра D следует одновременно использовать значения
Iвх и Iвых, на взаимопротивоположных точках поверхностей мембраны. Дополнительным преимуществом этого способа является отсутствие необходимости калибровки по абсолютной активности, т. е. определения параметра
А в уравнении (1).
). Действительно, разброс значений
Iвых, в известном смысле отражает развитие диффузионного процесса на конкретном участке мембраны. Однако такой подход возможен, только если неоднородность почернения связана исключительно с, неоднородностью диффузионного процесса. В случае наличия спектра констант растворимости
Кр плотность почернения Iвых
~ КрD, и для расчета спектра D следует одновременно использовать значения
Iвх и Iвых, на взаимопротивоположных точках поверхностей мембраны. Дополнительным преимуществом этого способа является отсутствие необходимости калибровки по абсолютной активности, т. е. определения параметра
А в уравнении (1).
Для облегчения расчета параметра и нами протабулированы функции
F(u)= Iвх / Iвых для различных значений
m, x (рис. 4, а) и Rх, (рис. 4, б). Как следует из рис. 4, существует определенный интервал значений
F (u), который является оптимальным с точки зрения определения
u. Этот интервал зависит от сочетания величин Н,
t и m (или Ra). При больших значениях пробега (малых
H или малых m) основной вклад в засветку обеих фотопластинок вносит
С0 и определить D практически невозможно. При малых значениях пробега (Н > 2R) излучение из центральной части мембраны уже не достигает фотопластинок и информация о распределении концентрации в этой части мембраны становится недоступной.
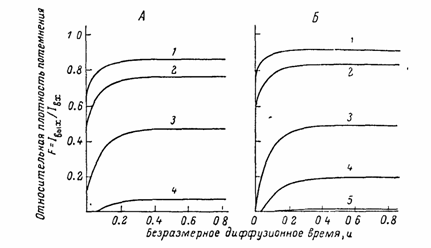 Рис. 4. Теоретические кривые зависимости
F(u) = Iвых/Iвх от безразмерного диффузионного времени.
a -
b-излучение: 1 -
m = 10-4; 2 – 10-3; 3 – 10-1; б -
a-излучение: 1 - Ra=500; 2 – 250; 3 – 100; 4 – 50; 5 – 5 мкм.
Рис. 4. Теоретические кривые зависимости
F(u) = Iвых/Iвх от безразмерного диффузионного времени.
a -
b-излучение: 1 -
m = 10-4; 2 – 10-3; 3 – 10-1; б -
a-излучение: 1 - Ra=500; 2 – 250; 3 – 100; 4 – 50; 5 – 5 мкм.
В результате точность расчета D снижается. При очень низких значениях пробега и при малых временах диффузии
F(u)® 0 и поэтому также нельзя рассчитать
D. При больших временах (больших u), по мере приближения к стационарному состоянию, система становится неустойчивой, поскольку небольшие флуктуации в
F(u) приводят к большим отклонениям
u. В области стационарного состояния определить
D вообще не удастся, так как в этом случае распределение концентрации не зависит от
D, а определяется только разностью концентраций на входной и выходной поверхности мембраны. Таким образом, при каждых конкретных условиях эксперимента существует определенный интервал времен, при которых возможно падежное определение диффузионных параметров. В связи с этим желательно иметь несколько АРГ, снятых с одного участка образца, но при различных временах диффузии.
Такой набор данных необходим и в тех случаях, когда затруднено определение коэффициента ослабления (или пробега) излучения в веществе. Способ обработки результатов, не требующий знания
m (или Rx), основан па том факте, что при сравнительно больших временах диффузии (но еще вдали от стационарного состояния) в уравнении (4) можно ограничиться первым членом ряда. Тогда
 |
(7) |
После преобразования получим
|
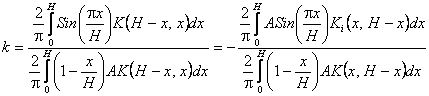 |
(8) |
После преобразования получим
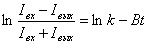 |
(9) |
В параметре k собраны все величины, связанные с поглощением излучения материалом образца. Угловой коэффициент
В выведенного уравнения (9) зависит только от диффузионных факторов. Из графика, построенного в координатах ln(Iвх-Iвых/
Iвх+Iвых) от t найдем D по наклону прямой к оси абсцисс.
В предварительных экспериментах, проведенных традиционным вариантом метода проницаемости, была изучена диффузия радона через полипропиленовую мембрану толщиной
H=110 мкм. Кинетические кривые «прорыва» обрабатывали по стандартной методике с использованием метода наименьших квадратов. Обнаружено хорошее согласие экспериментальных результатов с теоретическими зависимостями: каких-либо аномалий, свидетельствующих о наличии нескольких коэффициентов диффузии, не наблюдалось. Коэффициент диффузии
D =(11.5±0.5)×10-9 см2/с.
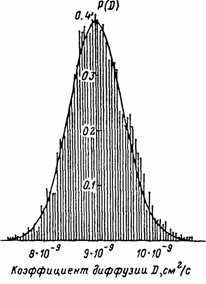 Рис. 5. Плотность распределения выборки из коэффициентов диффузии радона в полипропилене.
Рис. 5. Плотность распределения выборки из коэффициентов диффузии радона в полипропилене.
При работе но авторадиографическому варианту А диффузионный эксперимент прерывали при времени
t = t1/2 мембрану вынимали и зажимали между двумя фотопластинками. Из данных фотометрирования по площади па входной и выходной поверхностях мембраны вычисляли
Fэксп и, пользуясь предварительно рассчитанной зависимостью Fтеор, находили массив
u. Сводные результаты расчетов приведены на рис. 5. Видно, что плотность распределения выборки хорошо соответствует нормальному распределению (основные моменты экспериментального распределения
b1=0.01; b2=2.98, тогда как соответствующие значения для гауссовского распределения
b1=0; b2=З). Средний коэффициент диффузии из данных АРГ
D = (9±l)×10-9 см2/с.
Таким образом, коэффициенты диффузии, полученные по двум способам авторадиографического варианта метода проницаемости, в пределах ошибки эксперимента согласуются как между собой, так и с данными традиционного варианта метода проницаемости (хотя для АРГ они все же несколько ниже).
Отметим, что распределение
a-треков по поверхности мембраны было достаточно равномерным. Лишь при малых временах диффузии отмечено существование некоторой неоднородности на авторадиограмме, снятой с выходной поверхности образца. При больших временах на АРГ со входной поверхности появляются отдельные упорядоченные скопления типа «звезд», связанные, по-видимому, с отложением продуктов радиоактивного распада радона (так называемого «активного налета»).
Литература
- Голубев Б. П. Дозиметрия и защита от ионизирующих излучений. - М.: Атомиздат, 1976, с. 412.
- Иванов В. И. Дозиметрия ионизирующих излучений. — М.: Атомиздат, 1964, с. 250.
(Получено 28 VI 1980)
 Рис. 1. Устройство для одновременного использования метода газопроницаемости и метода авторадиографии
1 – зажимное устройство; 2 – диффузионная ячейка; 3 – термостатированный корпус; 4 – пористая керамика; 5 – фотопластинка с ядерной эмульсией; 6 – прокладка из губчатой резины; 7 – металлическая пластина; 8 – полимерная мембрана.
Рис. 1. Устройство для одновременного использования метода газопроницаемости и метода авторадиографии
1 – зажимное устройство; 2 – диффузионная ячейка; 3 – термостатированный корпус; 4 – пористая керамика; 5 – фотопластинка с ядерной эмульсией; 6 – прокладка из губчатой резины; 7 – металлическая пластина; 8 – полимерная мембрана.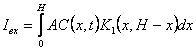
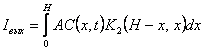
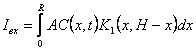
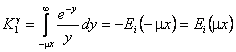
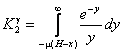
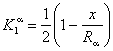
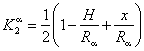
 Рис. 3. Зависимость плотностей почернения фотопластинки от безразмерного диффузионного времени.
1 — плотность почернения на входной стороне мембраны; 2 — плотность почернения на выходной стороне мембране; 3 — отношение плотности почернения на выходной стороне мембраны к плотности почернения на входной стороне мембраны. (14С,
Е
Рис. 3. Зависимость плотностей почернения фотопластинки от безразмерного диффузионного времени.
1 — плотность почернения на входной стороне мембраны; 2 — плотность почернения на выходной стороне мембране; 3 — отношение плотности почернения на выходной стороне мембраны к плотности почернения на входной стороне мембраны. (14С,
Е Рис. 4. Теоретические кривые зависимости
F(u)
Рис. 4. Теоретические кривые зависимости
F(u)
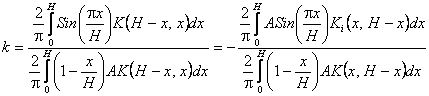
 Рис. 5. Плотность распределения выборки из коэффициентов диффузии радона в полипропилене.
Рис. 5. Плотность распределения выборки из коэффициентов диффузии радона в полипропилене.